Քառակուսի արմատի ֆունկցիան, նրա գրաֆիկն ու հատկությունները

y = \sqrt{x}

ֆունկցիայի գրաֆիկը կառուցելու համար, սովորականի պես, \(x\) անկախ փոփոխականին տանք մի քանի դրական արժեքներ (\(x < 0\) դեպքում

\sqrt{x}

իմաստ չունի) և հաշվենք \(y\) կախյալ փոփոխականի համապատասխան արժեքները: Հարմարության համար կընտրենք \(x\) -ի այնպիսի արժեքներ, որոնց դեպքում ճշգրիտ որոշվում է քառակուսի արմատի արժեքը: Այսպիսով՝

եթե \(x=0\), ապա

y = \sqrt{0} = 0

եթե \(x=1\), ապա

y = \sqrt{1} = 1

եթե \(x=4\), ապա

y = \sqrt{4} = 2

եթե \(x=6,25\), ապա

y = \sqrt{6.25} = 2.5

եթե \(x=9\), ապա

y = \sqrt{9} = 3

Արդյունքում, լրացրինք հետևյալ աղյուսակը:

\(x\)	\(0\)	\(1\)	\(4\)	\(6.25\)	\(9\)
\(y\)	\(0\)	\(1\)	\(2\)	\(2.5\)	\(3\)

Կոորդինատական հարթության վրա կառուցենք գտնված \((0; 0), (1;1), (4; 2), (6.25; 2.5), (9;3)\) կետերը: Դրանք գտնվում են որոշ կորի վրա: Գծենք այն:

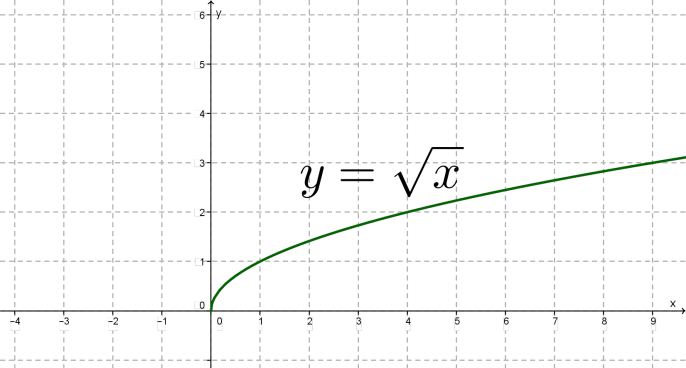
Ստացանք

y = \sqrt{x}

ֆունկցիայի գրաֆիկը:

Ուշադրություն

Գրաֆիկը շոշափում է \(y\) -երի առանցքը \((0; 0)\) կետում:

y = \sqrt{x}

ֆունկցիայի հատկությունները

Հատկությունները թվարկելիս կհիմնվենք կառուցված գրաֆիկի վրա:

1. Ֆունկցիայի որոշման տիրույթը

[0; + \infty)

ճառագայթն է:

2. \(y = 0\) եթե \(x = 0\) և \(y >\)0 եթե \(x > 0\)

3. Ֆունկցիան աճում է

[0; + \infty)

ճառագայթի վրա:

4. Ֆունկցիան սահմանափակ է ներքևից, բայց սահմանափակ չէ վերևից:

5. Ֆունկցիան ունի փոքրագույն արժեք և չունի մեծագույն արժեք

y_{\min} = 0, եթե x = 0 և y_{\max} գոյություն չունի

6. Ֆունկցիան անընդհատ է

[0; + \infty)

ճառագայթի վրա:

7. Ֆունկցիայի արժեքների բազմությունը օրդինատների առանցքի դրական ճառագայթն է՝

[0; + \infty)

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Քառակուսի արմատի ֆունկցիան, նրա գրաֆիկն ու հատկությունները

Տեսություն