1. Երկու անհայտներով գծային հավասարում

Երկու անհայտներով գծային հավասարում
ax+by+c=0 տեսքի հավասարումը, որտեղ \(a -ն, b -ն, c -ն\) թվեր են (գործակիցներ), կոչվում է \(x\) և \(y\) երկու անհայտներով առաջին աստիճանի գծային հավասարում: \(a\) և \(b\) թվերը կոչվում են անհայտների գործակիցներ, իսկ \(c\)-ն՝ ազատ անդամ: 
 ax+by+c=0 հավասարման լուծում անվանում են ցանկացած (\(x\);\(y\)) թվազույգ, որը բավարարում է ax+by+c=0 հավասարմանը, այսինքն՝ հավասարման մեջ տեղադրելիս այն վերածում է ճիշտ թվային հավասարության:
Օրինակ
Նկարագրենք x+y−3=0 երկու անհայտով գծային հավասարման լուծումների դիրքը \(xOy\) կոորդինատային հարթության վրա:
Վերցնենք հավասարման մի քանի լուծում, այսինքն, դիտարկենք մի քանի թվազույգեր, որոնք բավարարում են տրված հավասարմանը՝ \((3;0), (2;1), (1;2), (0;3), (4;-1)\)
 
Կառուցենք այդ կետերը \(xOy\) կոորդինատային հարթության վրա:
 
Նկատում ենք, որ դրանք բոլորն ընկած են միևնույն \(t\) ուղղի վրա:
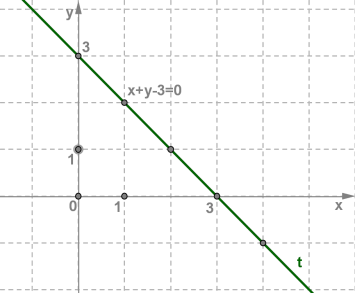
lineara teorija.png
 
Այսպիսով, x+y−3=0 հավասարման լուծումները հարթության վրա կազմում են \(t\) ուղիղը: 
 
Այսինքն, եթե (\(x\);\(y\)) կետը բավարարում է ax+by+c=0 հավասարմանը, ապա \(М\)(\(x\);\(y\)) կետն ընկած է \(t\) ուղղի վրա, և, հակառակը, եթե \(М\)(\(x\);\(y\)) կետն ընկած է \(t\) ուղղի վրա, ապա (\(x\);\(y\)) թվազույգը բավարարում է ax+by+c=0 հավասարմանը:
 
Տեղի ունի հետևյալ թեորեմը.
Եթե ax+by+c=0 գծային հավասարման \(a, b\) գործակիցներից գոնե մեկը տարբեր է զրոյից, ապա հավասարումն ունի անվերջ թվով լուծումներ, որոնք ընկած են միևնույն ուղղի վրա: 
 ax+by+c=0 հավասարման բոլոր լուծումները գտնելու համար պետք է կառուցել այդ ուղիղը:
 
Դիտարկենք a≠0,b≠0 դեպքը: Կատարենք հետևյալ քայլերը:
  
1. Վերցնենք \(x\) փոփոխականի որոշակի արժեք՝ x=x1 և ax1+by+c=0 հավասարումից գտնենք y=y1 արժեքը:
  
2. Վերցնենք \(x\) փոփոխականի մեկ ուրիշ x=x2 արժեք և ax2+by+c=0 հավասարումից գտնենք y=y2 արժեքը:
3. \(xOy\) կոորդինատային հարթության վրա կառուցենք x1;y1x2;y2 կետերը:
4. Այդ կետերով տանենք ուղիղ:
 
Դա հենց կլինի ax+by+c=0 հավասարման բոլոր լուծումները նկարագրող ուղիղը՝ հավասարման գրաֆիկը: 
Օրինակ
Կառուցենք x−2y−4=0 հավասարման գրաֆիկը: Կառուցումը կատարենք ըստ թվարկված քայլերի: 
 
1. Վերցնենք \(x = 0\) արժեքը: Կստանանք՝ 
 
0−2y−4=0,−2y=4,y=4:−2y=−2
 
2. Վերցնենք \(y = 0\) արժեքը: Կստանանք՝
 
x−2⋅0−4=0x−4=0x=4
 
3. Կառուցենք \(xOy\) հարթության վրա ստացված \((0;-2)\) և \((4;0)\) կետերը:
 
4. Այդ կետերով տանենք ուղիղ:
 
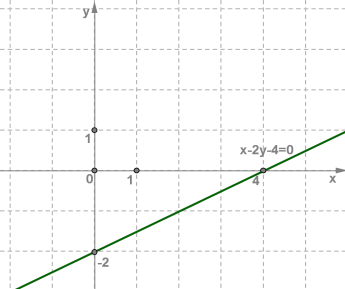
lineara1.png
 
Այս ուղղի վրա են գտնվում x−2y−4=0 հավասարման բոլոր լուծումները:
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:
Վերադառնալ թեմային
Հաջորդ առաջադրանքը
Copyright © 2024 ԻմԴպրոց ՍՊԸ