
















Միանուն և կրկնակի անհավասարումներ
\(a>b\) և \(c>d\) կամ \(a<b\) և \(c<d\) անհավասարությունները (միևնույն նշանի) կոչվում են միանուն:
\(a>b\) և \(c<d\) կամ \(a<b\) և \(c>d\) անհավասարությունները (հակառակ նշանի) կոչվում են հականուն:
Օրինակ
\(x>-5\) և \(y>17\) անհավասարությունները միանուն են, իսկ \(x< - 5\) և \(y>17\) անհավասարությունները՝ հականուն:
Օրինակ, դա կարելի է անել թվային առանցքի վրա լուծումների միջակայքը պատկերելով և օգտագործելով պատկանելիության նշանը:
| \(x > a\) անհավասարման լուծումները պատկերում են այսպես՝ |  | |
| անհավասարման լուծումները պատկերում են այսպես՝ |  | |
| անհավասարման լուծումները պատկերում են այսպես՝ |  | |
\(x < a\) անհավասարման լուծումները պատկերում են այսպես՝ |  |
Եթե միաժամանակ տեղի ունեն երկու պայման՝ \(x>a\) () և \(x<b\) (), ապա ասում են, որ տրված է կրկնակի անհավասարում և գրում են՝ \(a<x<b\)
\(a< x <b\) կրկնակի անհավասարմանը բավարարող \(x\) թվերի բազմությունը կարելի է պատկերել թվային առանցքի վրա:
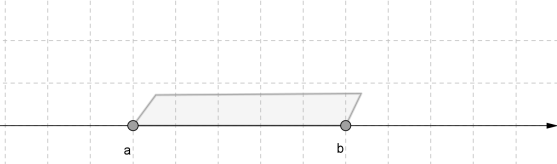
Կրկնակի անհավասարումը կարդում ենք մեջտեղից՝ \(x\) -ը մեծ է \(a\) -ից, բայց փոքր է \(b\) -ից:
Օրինակ՝ կարդում ենք՝ \(x\) -ը մեծ է \(47,2\) -ից, բայց փոքր է \(47,3\) -ից:
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012: