
















Գծային ֆունկցիան և նրա գրաֆիկը
\(y = kx + b\) տեսքի ֆունկցիան, որտեղ \(k\)-ն և \(b\)-ն տրված թվեր են, անվանում են գծային ֆունկցիա:
\(y = kx+b\) ֆունկցիան իմաստ ունի ցանկացած \(x\)-ի համար՝ ունենալով \(x\)-ի ցանկացած արժեք, բանաձևի օգնությամբ, կարելի է հաշվել \(y\)-ի համապատասխան արժեքը: Սա նշանակում է, որ \(y = kx+b\) ֆունկցիայի որոշման տիրույթը բոլոր իրական թվերի բազմությունն է:
Եթե \(b = 0\), ապա ստանում ենք \(y = kx\) ուղիղ համեմատականության ֆունկցիան:
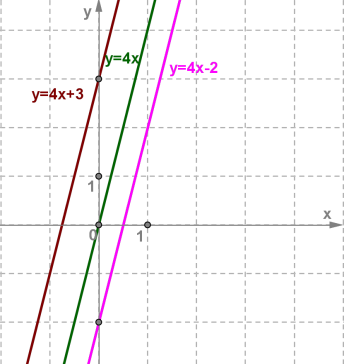
Կառուցենք \(y = 4x+3\) ֆունկցիայի գրաֆիկը: Նախ կառուցենք \(y = 4x\) ֆունկցիայի գրաֆիկը: Արդեն գիտենք, որ դա \((0; 0)\) կետով անցնող ուղիղ գիծ է:
Համեմատելով \(y = 4x+3\) և \(y = 4x\) բանաձևերը՝ նկատում ենք, որ նույն \(x\)-ի համար \(y = 4x+3\) ֆունկցիայի \(y\)-ը \(3\)-ով մեծ է \(y = 4x\) ֆունկցիայի \(y\)-ից: Սա նշանակում է, որ եթե \((x; y)-\)ը \(y = 4x\) ֆունկցիայի գրաֆիկի կետ է, ապա \(y = 4x+3\) գծային ֆունկցիայի գրաֆիկի համապատասխան կետը կունենա \((x; y+3)\) տեսքը:
Հետևաբար, գրաֆիկը կառուցելու համար կարելի է վարվել հետևյալ կերպ:
Տեղափոխենք \(y = 4x\) ֆունկցիայի գրաֆիկը դեպի վեր \(3\) միավորով՝ կստանանք \(y = 4x+3\) ֆունկցիայի գրաֆիկը: Այսպիսով՝
\(y = kx + b\) գծային ֆունկցիայի գրաֆիկը ուղիղ գիծ է, որը զուգահեռ է \(y = kx\) ֆունկցիայի գրաֆիկին և ստացվում է դրանից զուգահեռ տեղափոխությամբ \(b\) միավորով:
Նույն կերպ՝ զուգահեռ տեղափոխելով \(y = 4x\) ֆունկցիայի գրաֆիկը դեպի ներքև \(2\) միավորով՝ ստանում ենք \(y = 4x-2\) ֆունկցիայի գրաֆիկը (տես ներքևի նկարը):

Նկարի երեք ուղիղները իրար զուգահեռ են և ունեն նույն \(k = 4\) գործակիցը: Այդ պատճառով՝
\(y = kx + b\) գծային ֆունկցիայի \(k\) թիվը անվանում են անկյունային գործակից: Այսպիսով՝ նույն անկյունային գործակցով ուղիղները զուգահեռ են:
Եթե \(k>0\), ապա \(y = kx + b\) ուղիղը \(x\)-երի առանցքի դրական ուղղության հետ կազմում է սուր անկյուն, եթե \(k<0\), ապա այդ անկյունը բութ է:
Եթե \(y = kx+b\) բանաձևում տեղադրենք \(x\ = 0\), ապա կստանանք՝ \(y = b\): Այսպիսով՝
\((0;b)\) կետը միշտ պատկանում է \(y = kx+b\) գծային ֆունկցիայի գրաֆիկին, իսկ \(b\) թիվը ցույց է տալիս, թե որ կետում է ուղիղը հատում \(y\)-ների առանցքը:
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 7-րդ դասարան, Անտարես, 2011: