1. Թվային բազմությունների սահմանումները

Ռացիոնալ թվերի $\mathrm{\mathbb{Q}}$ բազմությունը բաղկացած է $\frac{m}{n};-\frac{m}{n}$ տեսքի թվերից (որտեղ \(m\)-ը և \(n\)-ը բնական թվեր են) և \(0\) թվից:

Հասկանալի է, որ՝ $\mathrm{\mathbb{N}}$ -ը $\mathrm{\mathbb{Z}}$ -ի ենթաբազմություն է, իսկ $\mathrm{\mathbb{Z}}$ -ը՝ $\mathrm{\mathbb{Q}}$ -ի: $\mathrm{\mathbb{N}}\subset \mathrm{\mathbb{Z}};\mathrm{\mathbb{Z}}\subset \mathrm{\mathbb{Q}}$

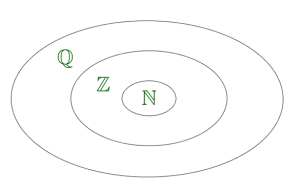
Ցանկացած ռացիոնալ թիվ կարելի է ներկայացնել պարբերական տասնորդական կոտորակի տեսքով (վերջավոր կամ անվերջ)՝

$\begin{array}{l}4=\mathrm{4,000}...=\mathrm{4,}(0)\\ \frac{5}{4}=1,25=1,\mathrm{25000...}=1,25(0)\\ \frac{7}{22}=\mathrm{0,3181818}...=\mathrm{0,3}(18)\\ \mathrm{7,3777}=\mathrm{7,37770000}...=\mathrm{7,3777}(0)\end{array}$

Ճիշտ է նաև հակառակ պնդումը՝ ցանկացած պարբերական տասնորդական կոտորակ ռացիոնալ թիվ է: 

Սակայն, կան անվերջ տասնորդական կոտորակներ, որոնք պարբերական չեն: