Կոմպլեքս թվի եռանկյունաչափական տեսքը — դաս։ Հանրահաշիվ, 10-րդ դասարան.

Դիցուք կոմպլեքս հարթության վրա պատկերված է \(z = a + bi\) կոմպլեքս թիվը:

\(z\) կոմպլեքս թվի արգումենտ կոչվում է այն պտտման անկյունը, որով աբսցիսների դրական կիսաառանցքը պտտելով՝ կստանանք \(Oz\) ճառագայթը:

\(z\) թվի արգումենտը նշանակում են \(arg z\)

Կոմպլեքս թվի արգումենտը միարժեքորեն չի որոշվում:

Պարզ է, օրինակ, որ

\arg 1 = 0 և \arg 1 = 2 π

և այլն:

\(z\) թվի արգումենտը իրարից տարբերվում են

2 π k

-ով,

k \in ℤ

Եթե

z = a + bi, r = |z|, ϕ = \arg z

, ապա

r = \sqrt{a^{2} + b^{2}}, a = r \cos ϕ, b = r \sin ϕ

Տեղադրելով \(z = a + bi\) հավասարության մեջ, ստանում ենք՝

z = r (\cos ϕ + i \sin ϕ)

z = r (\cos ϕ + i \sin ϕ)

բանաձևը կոչվում է \(z\) կոմպլեքս թվի եռանկյունաչափական տեսք:

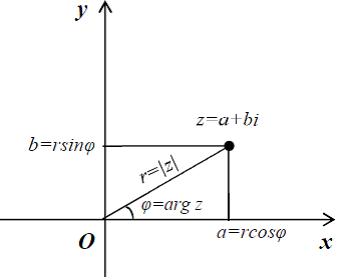
Հեշտ է նկատել, որ

\begin{array}{l} 1 = 1 \cdot (\cos 0 + i \sin 0), - 1 = 1 \cdot (\cos π + i \sin π), \\ i = 1 \cdot (\cos \frac{π}{2} + i \sin \frac{π}{2}), - i = 1 \cdot (\cos \frac{3 π}{2} + i \sin \frac{3 π}{2}) \end{array}

Օրինակ

Գտնենք

z = 12 - 5 i

թվի եռանկյունաչափական տեսքը:

Հաշվենք \(z\) թվի մոդուլը՝

|z| = |12 - 5 i| = \sqrt{12^{2} + {(- 5)}^{2}} = 13

\(z\) թիվը ներկայացնենք հետևյալ տեսքով՝

12 - 5 i = 13 \cdot (\frac{12}{13} - i \frac{5}{13})

Նկատենք, որ եթե նշանակել

ϕ = - \arccos \frac{12}{13}

, ապա

\cos ϕ = \frac{12}{13}, \sin ϕ = - \frac{5}{13}

Հետևաբար,

12 - 5 i = 13 \cdot (\cos ϕ + i \sin ϕ)

, որտեղ

ϕ = - \arccos \frac{12}{13}

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

1. Կոմպլեքս թվի եռանկյունաչափական տեսքը