1. Կոմպլեքս հարթություն

Յուրաքանչյուր \(z = a + bi\) կոմլեքս թվի համապատասխանեցնենք կոորդինատային հարթության \((a; b)\) կետը, որի աբսցիսը \(z\)-ի իրական մասն է, իսկ օրդինատը՝ կեղծ մասի գործակիցը:

 

 

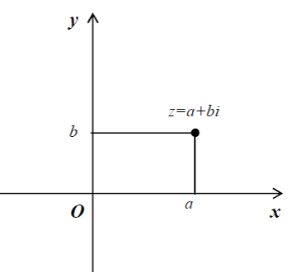
Պարզ է, որ հարթության յուրաքանչյուր կետի համապատասխանում է որևէ կոմպլեքս թիվ: Այսպիսով, ստեղծվում է փոխմիարժեք արտապատկերում կոմպլեքս թվերի և կոորդինատային հարթության կետերի միջև:

Պարզ է, որ աբսցիսների առանցքի վրա գտնվում են իրական թվերը, իսկ օրդինատների առանցքի վրա՝ կեղծ թվերը: Ուստի,

Ընդունված է կոմպլեքս թիվը և կոմպլեքս հարթության վրա նրան համապատասխանող կետը նույնացնել՝ $z=a+\mathit{bi}=\left(a;b\right)$

 

Օրինակ՝ $1=\left(1;0\right),2=\left(2;0\right),-1=\left(-1;0\right)$ կետերը գտնվում են իրական (աբսցիսների) առանցքի վրա և պատկերում են իրական թվեր:

 

$i=\left(0;1\right),-i=\left(0;-1\right),2i=\left(0;2\right)$ կետերը գտնվում են կեղծ (օրդինատների) առանցքի վրա և պատկերում են կեղծ թվեր:

Իրոք, \(z = a + bi\) կոմլեքս թվին համապատասխանող \((a; b)\) կետի հեռավուրությունը կոորդինատների \((0; 0)\) սկզբնակետից հավասար է $\sqrt{a^2+b^2}$, այսինքն $\left|z\right|$-ի: