Պարբերական ֆունկցիաներ — դաս։ Հանրահաշիվ, 10-րդ դասարան.

Ասում են, որ \(y=f(x)\),

x \in X

ֆունկցիան ունի \(T\) պարբերություն, եթե կամայական

x \in X

արգումենտի համար տեղի ունեն հետևյալ հավասարությունները՝

f (x - T) = f (x) = f (x + T)

Զրոյից տարբեր \(T\) պարբերություն ունեցող ֆունկցիան կոչվում է պարբերական:

Եթե \(y=f(x)\),

x \in X

ֆունկցիան ունի \(T\) պարբերություն, ապա \(T\)-ին պատիկ ցանկացած թիվ ևս \(y=f(x)\) ֆունկցիայի պարբերությունն է:

Պարբերական ֆունկցիան ունի անվերջ թվով պարբերություններ:

Մեծամասամբ դրանց մեջ լինում է ամենափոքր դրական պարբերությունը:

Եթե պարբերական ֆունկցիան ունի փոքրագույն դրական պարբերություն, ապա այն անվանում են հիմնական պարբերություն:

Պարբերական ֆունկցիայի լավ օրինակներ են \(y = sin x\) և \(y = cos x\) եռանկյունաչափական ֆունկցիաները: Դրանց պարբերությունը հավասար է

2 π

\(y = tg x\) և \(y = ctg x\) ֆունկցիաները ևս պարբերական են՝

π

պարբերությամբ:

Նույնաբար հաստատուն \(y = const\) ֆունկցիան ևս պարբերական է: Նրա համար ցանկացած

T \neq 0

թիվ պարբերություն է:

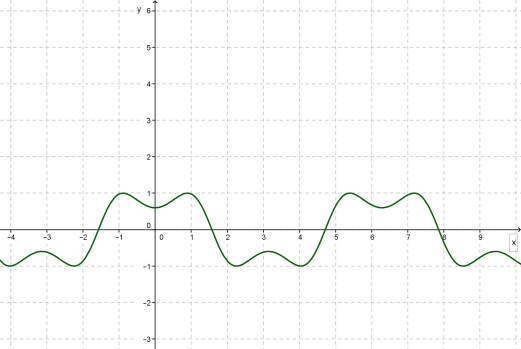
Պարբերական ֆունկցիայի գրաֆիկը սովորաբար կառուցում են

[x_{0}; x_{0} + T)

հատվածի վրա, ապա այն կրկնելով շարունակում են ամբողջ որոշման տիրույթի վրա:

Հետևյալը

y = \sin (\frac{5}{2} \cos x)

ֆունկցիայի գրաֆիկն է:

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

1. Պարբերական ֆունկցիաներ