Հակադարձ ֆունկցիա — դաս։ Հանրահաշիվ, 10-րդ դասարան.

\(y = f(x)\),

x \in X

ֆունկցիան անվանում են հակադարձելի \(X\) բազմությունում, եթե այն իր յուրաքանչյուր արժեք ընդունում է \(X\) բազմության միայն մեկ կետում (այլ բառերով՝ արգումենտի իրարից տարբեր արժեքներին համապատասխանում են ֆունկցիայի իրարից տարբեր արժեքներ):

Թեորեմ 1

Եթե \(y=f(x)\),

x \in X

ֆունկցիան մոնոտոն է, ապա այն հակադարձելի է \(X\) բազմությունում:

Հիշենք, որ մոնոտոն ֆունկցիան աճում կամ նվազում է խիստ իմաստով:

Դիցուք \(y = f(x)\)-ը, հակադարձելի ֆունկցիա է \(X = D(f)\) որոշման տիրույթով և \(Y = E(f)\) արժեքների բազմությամբ: Յուրաքանչյուր \(y\)-ի \(Y\) բազմությունից համապատասխանության մեջ դնենք այն միակ \(x\)-ը \(X\) բազմությունից, որի դեպքում տեղի ունի

f (x) = y

հավասարությունը (այսինքն,

f (x) = y

հավասարման միակ լուծումը \(x\)-ի նկատմամբ): Ստանում ենք ֆունկցիա, որի որոշման տիրույթը \(Y\) բազմությունն է, իսկ արժեքների բազմությունը՝ \(X\)-ը: Այդ ֆունկցիան նշանակում են

x = f^{- 1} (y), y \in Y

և անվանում են \(y = f(x)\),

x \in X

ֆունկցիայի հակադարձ ֆունկցիա:

Հակադարձ ֆունկցիայի արժեքը \(Y\) բազմության \(y\) կետում հավասար է այն \(x\)-ին \(X\) բազմությունից, որի համար \(f(x) = y\), այսինքն՝

f^{- 1} (y) = f^{- 1} (f (x)) = x

Թեորեմ 2

Եթե \(y=f(x)\) ֆունկցիան աճում է (նվազում է) \(X\) բազմությունում, և \(Y\)-ը նրա արժեքների բազմությունն է, ապա

x = f^{- 1} (y), y \in Y

հակադարձ ֆունկցիան աճում է (նվազում է) \(Y\) բազմությում:

Թեորեմ 3

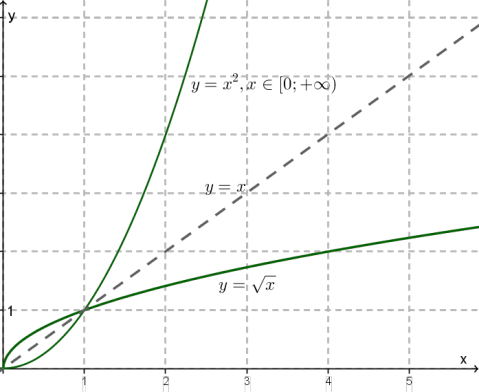
\(y=f(x)\) ֆունկցիայի և նրա հակադարձ ֆունկցիայի գրաֆիկները համաչափ են \(y=x\) առանցքի նկատմամբ:

Հակադարձ ֆունկցիայի բանաձևը

\(y = f(x)\) ֆունկցիայի հակադարձ ֆունկցիայի բանաձևը գտնելու համար պետք է.

ա) \(y = f(x)\) հավասարումից (x\)-ն արտահայտել \(y\)-ով,

բ) ստացված \(x = g(y)\) բանաձևում փոխել \(x\)-ի և \(y\)-ի տեղերը:

Գտնենք

y = x^{2}, x \in [0; + \infty)

ֆունկցիայի հակադարձ ֆունկցիան:

Օրինակ

Տրված ֆունկցիան աճում է

[0; + \infty)

բազմությունում, հետևաբար, այն հակադարձելի է:

y = x^{2}

հավասարումից գտնում ենք՝

x = \sqrt{y}

կամ

x = - \sqrt{y}

, և քանի որ պետք են միայն դրական արժեքները, ապա ընտրում ենք

x = \sqrt{y}

արժեքը:

Փոխենք \(x\)-ի և \(y\)-ի տեղերը: Ստանում ենք՝

y = \sqrt{x}, x \in [0; + \infty)

Այս ֆունկցիայի գրաֆիկը համաչափ է

y = x^{2}, x \in [0; + \infty)

ֆունկցիայի գրաֆիկին \(y=x\) ուղղի նկատմամբ:

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Հակադարձ ֆունկցիա

Տեսություն