Ֆունկցիայի մոնոտոնության միջակայքեր — դաս։ Հանրահաշիվ, 10-րդ դասարան.

\(y=f(x)\) ֆունկցիան կոչվում է \(X\) բազմությունում աճող, եթե ցանկացած

x_{1}

x_{2}

թվերի համար \(X\) բազմությունից

x_{1} < x_{2}

անհավասարությունից հետևում է, որ

f (x_{1}) < f (x_{2})

\(y=f(x)\) ֆունկցիան կոչվում է \(X\) բազմությունում նվազող, եթե ցանկացած

x_{1}

x_{2}

թվերի համար \(X\) բազմությունից

x_{1} < x_{2}

անհավասարությունից հետևում է, որ

[5; 7]

Աճող և նվազող ֆունկցիաներն ունեն ընդհանուր անվանում՝ մոնոտոն ֆունկցիաներ:

Մեզ կհետաքրքրեն այն միջակայքերը, որտեղ \(y=f(x)\) ֆունկցիան մոնոտոն է:

Այդպիսի միջակայքը կոչվում է \(y=f(x)\) ֆունկցիայի մոնոտոնության միջակայք:

Օրինակ

ա)

f (x) = x^{2}

ֆունկցիան աճող է

[0; + \infty)

բազմության վրա:

բ)

f (x) = x^{2}

ֆունկցիան նվազող է

(- \infty; 0]

բազմության վրա:

Այսպիսով

f (x) = x^{2}

ֆունկցիայի մոնոտոնության միջակայքերն են՝

[0; + \infty)

(- \infty; 0]

Իհարկե

f (x) = x^{2}

ֆունկցիայի համար մոնոտոնության միջակայք է նաև, օրինակ,

[3; 8]

հատվածը, սակայն ֆունկցիայի մոնոտոնության միջակայքեր ընդունված է անվանել մեծագույն միջակայքերը, որոնց վրա ֆունկցիան մոնոտոն է:

Քանի որ ֆունկցիայի աճման և նվազման սահմանումների

f (x_{1}) < f (x_{2})

[5; 7]

անհավասարություններում բացառվում է հավասարության նշանը, ապա ֆունկցիաները նաև անվանում են խիստ աճող կամ խիստ նվազող (խիստ մոնոտոն):

Եթե այդ անհավասարություններում թույլ տանք նաև հավասարության նշանը, ապա կգանք ֆունկցիայի աճման և նվազման ոչ խիստ սահմանումներին:

\(y=f(x)\) ֆունկցիան կոչվում է չնվազող \(X\) բազմությունում, եթե ցանկացած

x_{1}

x_{2}

թվերի համար \(X\) բազմությունից

x_{1} < x_{2}

անհավասարությունից հետևում է, որ

f (x_{1}) \leq f (x_{2})

\(y=f(x)\) ֆունկցիան կոչվում է չաճող \(X\) բազմությունում, եթե ցանկացած

x_{1}

x_{2}

թվերի համար \(X\) բազմությունից

x_{1} < x_{2}

անհավասարությունից հետևում է, որ

f (x_{1}) \geq f (x_{2})

Գտնենք հետևյալ ֆունկցիայի մոնոտոնության միջակայքերը`

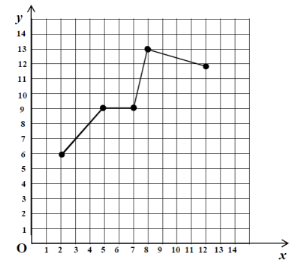
Գրաֆիկից տեսնում ենք, որ՝

[2; 5] և [7; 8]

հատվածներում ֆունկցիան խիստ աճող է,

[8; 12]

հատվածում ֆունկցիան խիստ նվազող է,

իսկ

[2; 8]

հատվածում ֆունկցիան չնվազող է (աճող է ոչ խիստ իմաստով), քանի որ

[5; 7]

հատվածում այն նույնաբար հաստատուն է:

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

1. Ֆունկցիայի մոնոտոնության միջակայքեր