1. Եռանկյունաչափական հիմնական նույնությունները

Միավոր շրջանագծի վրա վերցնենք \(A(x;y)\) կետը:

 

 

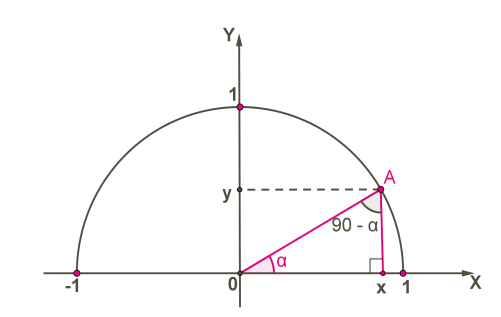
Համաձայն եռանկյունաչափական ֆունկցիաների սահմանման՝

 

 

Այսպիսով՝ $A\left(\mathit{cos}\mathrm{\alpha };\mathit{sin}\mathrm{\alpha }\right)$

 

Այստեղից հետևում է, որ՝

 

 

Այս հավասարությունները ճիշտ բոլոր այն անկյունների համար, որոնց դեպքերում, եռանկյունաչափական ֆունկցիաներն իմաստ ունեն և հայտարարները զրո չեն դառնում:

 

Հաշվի առնելով, որ \(A(x;y)\) կետը գտնվում է միավոր շրջանագծի վրա, այսինքն՝ $x^2+y^2=1$, կամայական $\mathrm{\alpha }$-ի համար ստանում ենք՝

 

 

Այս հավասարությունը կոչվում է եռանկյունաչափական հիմնական նույնություն:

 

Եթե ${\mathit{sin}}^2\mathrm{\alpha }+{\mathit{cos}}^2\mathrm{\alpha }=1$ հիմնական նույնության երկու մասերը բաժանենք ${\mathit{cos}}^2\mathrm{\alpha }$-ի վրա, ապա կստանանք անկյան տանգենսը կոսինուսի հետ կապող հետևյալ բանաձևը՝

$1+{\mathit{tg}}^2\mathrm{\alpha }=\frac{1}{{\mathit{cos}}^2\mathrm{\alpha }}$,

 

որը ճիշտ է բոլոր անկյունների համար, որոնց դեպքում կոսինուսը զրո չէ:

 

Նույն կերպ, եթե բաժանենք ${\mathit{sin}}^2\mathrm{\alpha }$-ի վրա, ապա կստանանք անկյան կոտանգենսը սինուսի հետ կապող հետևյալ բանաձևը՝

 

$1+{\mathit{ctg}}^2\mathrm{\alpha }=\frac{1}{{\mathit{sin}}^2\mathrm{\alpha }}$,