Միավոր շրջանագծի կետերի կոորդինատները — դաս։ Հանրահաշիվ, 10-րդ դասարան.

Դիտարկենք միավոր շրջանագիծը՝ $(0;0)$ կենտրոնով և $1$ շառավղով:

Շրջանագծի ցանկացած կետ ունի իր կոորդինատները: Օրինակ՝ $A$ կետի կոորդինատներն են $(1;0)$

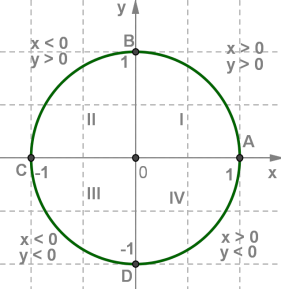
Գտնենք շրջանագծի այլ կարևոր կետերի կոորդինատները:

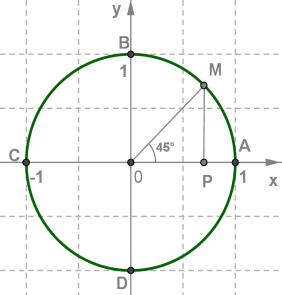Դիտարկենք նկարի

M

կետը:

$OA$ հատվածին

M

կետից իջեցնենք $MP$ ուղղահայացը և դիտարկենք $OMP$ ուղղանկյուն եռանկյունը:

Նկատենք, որ

∡ MOP = 45 °

կամ

\frac{π}{4}

ռադ:

Այսպիսով, $OMP$-ը հավասարասրուն ուղղանկյուն եռանկյուն է՝

$OP = MP$: Այսինքն, $M$ կետի կոորդինատները հավասար են՝ $x = y$:

Քանի որ $M(x;y)$ կետը գտնվում է շրջանագծի վրա, հետևաբար, նրա կոորդինատները պետք է բավարարեն շրջանագծի հավասարմանը՝

x^{2} + y^{2} = 1

Ուրեմն, կետի կոորդինատները գտնելու համար պետք է լուծել համակարգը՝

\{\begin{cases} x^{2} + y^{2} = 1 \\ x = y \end{cases}

Առաջին հավասարման մեջ $y$-ի փոխարեն տեղադրենք $x$ և լուծենք այն՝

\begin{array}{l} x^{2} + x^{2} = 1 \\ 2 x^{2} = 1 \\ x^{2} = \frac{1}{2} \\ x = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \\ y = x = \frac{\sqrt{2}}{2} \end{array}

Հաշվի առանք, որ $M$ կետի կոորդինատները դրական են:

Այսպիսով

\frac{π}{4}

ռադ անկյանը համապատասխանող $M$ կետի կոորդինատներն են՝

M (\frac{π}{4}) = M (\frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2})

Նկատենք, որ եթե

M (\frac{π}{4})

կետից միավոր շրջանագծի վրայով կատարենք լրիվ պտույտ՝ դրական կամ բացասական ուղղություններով (ժամացույցի սլաքի կամ նրան հակառակ ուղղությամբ), ապա կհայտնվենք նույն կետում:

Սա նշանակում է, որ

\frac{π}{4} + 2 π k, k \in ℤ

ռադ բոլոր անկյուններին ևս համապատասխանում է գտնված

M (\frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2})

կետը:

Նույն ձևով կարելի է հաշվել այլ կետերի կոորդինատներ, հաշվի առնելով դրանց կոորդինատների նշանները՝ կախված գտնվելու քառորդից:

Արդյունքները ներկայացնենք հետևյալ աղյուսակի տեսքով:

Շրջանագծի կետը

	$0$	$\frac{π}{4}$	$\frac{π}{2}$	$\frac{3 π}{4}$	$π$	$\frac{5 π}{4}$	$\frac{3 π}{2}$	$\frac{7 π}{4}$	$2 π$
Աբսցիցը՝ $x$	$1$	$\frac{\sqrt{2}}{2}$	$0$	$- \frac{\sqrt{2}}{2}$	$-1$	$- \frac{\sqrt{2}}{2}$	$0$	$\frac{\sqrt{2}}{2}$	$1$
Օրդինատը՝ $y$	$0$	$\frac{\sqrt{2}}{2}$	$1$	$\frac{\sqrt{2}}{2}$	$0$	$- \frac{\sqrt{2}}{2}$	$-1$	$- \frac{\sqrt{2}}{2}$	$0$

Նման ձևով գտնենք

\frac{π}{6}

ռադիան անկյանը համապատասխանող $M$ կետի կոորդինատները:

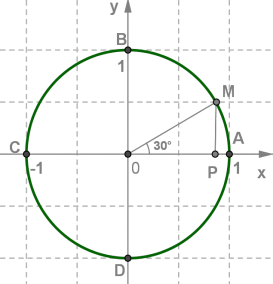$MOP$-ն ուղղանկյուն եռանկյուն է:

∡ MOP = 30 °

կամ

\frac{π}{6}

ռադ:

$MP$ էջը գտնվում է $30°$ անկյան դիմաց և հավասար է ներքնաձիգի կեսին՝

\begin{array}{l} MP = \frac{1}{2} \\ y = \frac{1}{2} \end{array}

$M$ կետի $x$ աբսցիսը գտնում ենք լուծելով հետևյալ հավասարումը՝

x^{2} + y^{2} = 1

\begin{array}{l} x^{2} = 1 - {(\frac{1}{2})}^{2} = 1 - \frac{1}{4} = \frac{3}{4} \\ x = \frac{\sqrt{3}}{2} \end{array}

Հաշվի առանք, որ $M$ կետի կոորդինատները դրական են:

Այսպիսով,

\frac{π}{6}

ռադիան անկյանը համապատասխանող $M$ կետի կոորդինատներն են՝

M (\frac{π}{6}) = M (\frac{\sqrt{3}}{2}; \frac{1}{2})

Արդեն նշել ենք, որ

\frac{π}{6} + 2 π k, k \in ℤ

տեսքի բոլոր անկյուններին ևս համապատասխանում է գտնված

M (\frac{\sqrt{3}}{2}; \frac{1}{2})

կետը:

Նույն ձևով կարելի է հաշվել այլ կետերի կոորդինատներ, հաշվի առնելով դրանց կոորդինատների նշանները՝ գտնվելու քառորդից կախված:

Արդյունքները ներկայացնենք հետևյալ աղյուսակի տեսքով:

Շրջանագծի կետը

	$\frac{π}{6}$	$\frac{π}{3}$	$\frac{2 π}{3}$	$\frac{5 π}{6}$	$\frac{7 π}{6}$	$\frac{4 π}{3}$	$\frac{5 π}{3}$	$\frac{11 π}{6}$
Աբսցիսը՝ $x$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$- \frac{1}{2}$	$- \frac{\sqrt{3}}{2}$	$- \frac{\sqrt{3}}{2}$	$- \frac{1}{2}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$
Օրդինատը՝ $y$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$- \frac{1}{2}$	$- \frac{\sqrt{3}}{2}$	$- \frac{\sqrt{3}}{2}$	$- \frac{1}{2}$

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Նախորդ տեսություն

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

3. Միավոր շրջանագծի կետերի կոորդինատները

Տեսություն