y=sinx ֆունկցիայի հատկություններն ու գրաֆիկը — դաս։ Հանրահաշիվ, 10-րդ դասարան.

y = sinx

ֆունկցիայի հատկությունները

Դիտարկենք

y = sinx

ֆունկցիան, որի արժեքը \(x\) կետում հավասար է \(x\) ռադիան անկյան սինուսին:

y = sinx

ֆունկցիայի որոշման տիրույթն ամբողջ թվային առանցքն է՝ \(D(sinx) =\)

ℝ

y = sinx

ֆունկցիայի արժեքների բազմությունը

[- 1; 1]

հատվածն է:

y = sinx

ֆունկցիան պարբերական է \(T =\)

2 π

պարբերությամբ:

y = sinx

ֆունկցիան կենտ է:

sinx = 0

, երբ

x = π n, n \in ℤ

y = sinx

ֆունկցիայի մեծագույն արժեքը \(1\)-ն է, որը ֆունկցիան ընդունում է

x = \frac{π}{2} + 2 π n, n \in ℤ

կետերում:

y = sinx

ֆունկցիայի փոքրագույն արժեքը \(-1\)-ն է, որը ֆունկցիան ընդունում է

x = - \frac{π}{2} + 2 π n, n \in ℤ

կետերում:

y = sinx

ֆունկցիան դրական է

(2 π n; π + 2 π n)

արգումենտների համար, և բացասական է

(π + 2 π n; 2 π + 2 π n)

արգումենտների համար, որտեղ

n \in ℤ

y = sinx

ֆունկցիան աճում է

[- \frac{π}{2} + 2 π n; \frac{π}{2} + 2 π n]

հատվածներում և նվազում է

[\frac{π}{2} + 2 π n; \frac{3 π}{2} + 2 π n]

հատվածներում, որտեղ

n \in ℤ

Հաշվի առնելով թվարկված հատկությունները, կառուցում ենք

y = sinx

ֆունկցիայի գրաֆիկը:

y = sinx

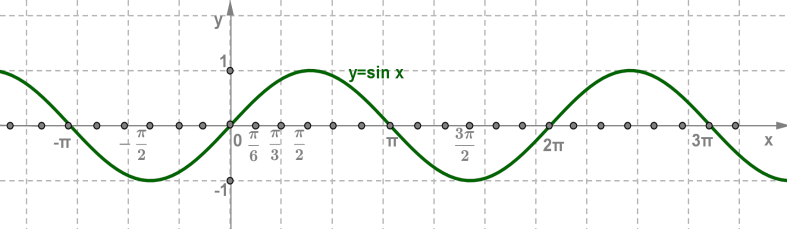
ֆունկցիայի գրաֆիկն անվանում են սինուսոիդա:

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

1. y=sinx ֆունկցիայի հատկություններն ու գրաֆիկը