y=ctgx ֆունկցիայի հատկություններն ու գրաֆիկը — դաս։ Հանրահաշիվ, 10-րդ դասարան.

y = ctgx

ֆունկցիան որոշված է

x \neq π n, n \in ℤ

արգումենտների համար, կենտ է և պարբերական՝

π

պարբերությամբ:

Ուստի, ֆունկցիայի գրաֆիկը բավական է կառուցել

(0; π)

բազմության վրա, ապա պարբերաբար շարունակել դեպի ձախ և աջ:

y = ctgx

ֆունկցիայի գրաֆիկը, երբ արգումենտը պատկանում է

(0; π)

միջակայքին, անվանում են կոտանգենսի գլխավոր ճյուղ:

y = ctgx

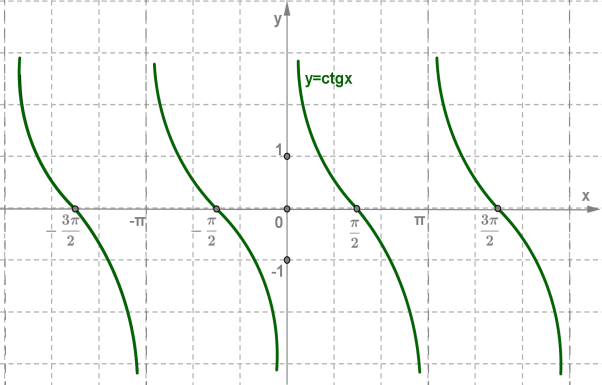
ֆունկցիայի հատկությունները

y = ctgx

ֆունկցիան որոշված է

x \neq π n, n \in ℤ

թվերի համար:

y = ctgx

ֆունկցիայի արժեքների բազմությունը ամբողջ թվային առանցքն է՝

E (ctgx) = ℝ

y = ctgx

-ը

π

-պարբերական ֆունկցիա է:

y = ctgx

-ը կետը ֆունկցիա է:

ctgx = 0

, եթե

x = \frac{π}{2} + π n, n \in ℤ

y = ctgx

ֆունկցիայի արժեքները դրական են

(π n; \frac{π}{2} + π n), n \in ℤ

միջակայքերում և բացասական են

(\frac{π}{2} + π n; π + π n), n \in ℤ .

միջակայքերում:

y = ctgx

ֆունկցիան նվազում է

(π n; π + π n), n \in ℤ .

միջակայքերում:

y = ctgx

ֆունկցիան էքստրեմումի կետեր չունի:

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

1. y=ctgx ֆունկցիայի հատկություններն ու գրաֆիկը