Ներդաշնակ տատանումների գրաֆիկը — դաս։ Հանրահաշիվ, 10-րդ դասարան.

Եռանկյունաչափական ֆունկցիաները օգտագործվում են տատանողական շարժումներ նկարագրելու համար:

Ամենակարևոր տատանողական գործընթացներից են

x (t) = Acos (ω t + α)

y (t) = Asin (ω t + α)

բանաձևերով նկարագրվող տատանողական շարժումները, որոնք անվանում են ներդաշնակ տատանումները:

Մասնավորապես, երբ կետը պտտվում է շրջանագծով, ապա նրա պրոյեկցիան աբսցիսների առանցքի վրա շարժվում է

x (t) = Acos (ω t + α)

օրենքով, իսկ պրոյեկցիան օրդինատների առանցքի վրա՝

y (t) = Asin (ω t + α)

օրենքով:

Երկու պրոյեկցիաներն էլ տատանվում են \([-A; A]\) սահմաններում:

Բերված բանաձևերում

A, ω, α

մեծությունները ունեն իրենց ֆիզիկական իմաստները:

\(A\)-ն (կամ \(-A\)-ն, եթե \(A<0\)) տատանումների ամպլիտուդն է (մեծագույն շեղումը հավասարակշռության դիրքից):

ω

-ն տատանումների անկյունային հաճախականությունն է:

α

-ն տատանումների սկզբնական փուլն է:

Օրինակ

Դիտարկենք

x (t) = 3 \cos (2 t + \frac{π}{3})

y (t) = 3 \sin (2 t + \frac{π}{3})

հավասարումներով տրված ներդաշնակ տատանումները և կառուցենք օրինակ՝ \(y(t)\) ֆունկցիայի գրաֆիկը:

Սկզբում ձևափոխենք ֆունկցիայի բանաձևը՝

y (t) = 3 \sin (2 t + \frac{π}{3}) = 3 \sin 2 (t + \frac{π}{6})

Պետք է հերթականությամբ կատարել

y = sint

սինուսոիդի հետևյալ ձևափոխությունները՝

1. \(2\) անգամ սեղմել դեպի օրդինատների առանցքը,

2. \(3\) անգամ ձգել աբսցիսների առանցքի երկայնքով,

3. տեղաշարժել

\frac{π}{6}

միավորով դեպի ձախ:

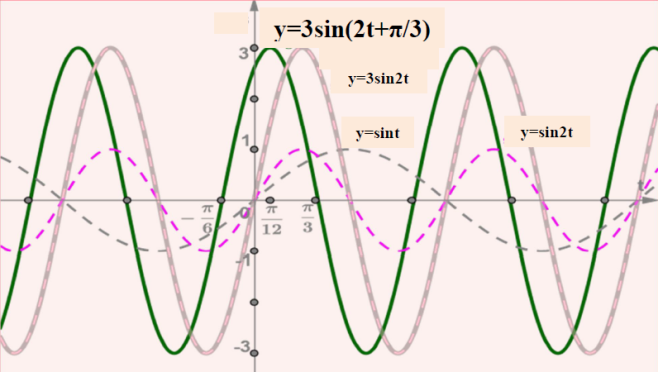
Արդյունքում ստանում ենք հետևյալ գրաֆիկը՝

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

1. Ներդաշնակ տատանումների գրաֆիկը