
















Առարկայի պատկերի կառուցումը բարակ ոսպնյակում: Բարակ ոսպնյակի բանաձևը:
Տարբեր օպտիկական սարքերում կիրառվող ոսպնյակները թույլ են տալիս ոչ միայն հավաքել կամ ցրել լուսային ճառագայթները, այլև ստանալ առարկաների զանազան՝ մեծացած կամ փոքրացած, ուղիղ կամ շրջված, իրական կամ կեղծ պատկերները:

Պարզվում է, որ ստացված պատկերի բնույթը կախված է ոսպնյակի տեսակից, ինչպես նաև առարկայի և ոսպնյակի փոխդասավորությունից:
Ինչպես գիտենք մարմինները տեսանելի են, եթե արձակում են լուսային ճառագայթներ կամ անդրադարձնում են իրենց վրա ընկնող լուսային ճառագայթները: Ոսպնյակով անցնելիս այդ ճառագայթները կարող են զուգամիտել. նման դեպքում ճառագայթների հատման կետում կստացվի այն կետի իրական պատկերը, որտեղից դուրս էին եկել այդ ճառագայթները: Իսկ երբ ճառագայթները տարամիտում են, ապա նրանց շարունակությունների հատման կետում կստացվի այդ կետի կեղծ պատկերը:
Առարկայի տարբեր կետերի իրական (կամ կեղծ) պատկերների ամբողջությունը կոչվում է առարկայի իրական (կամ կեղծ) պատկեր:
Այդպիսի «հարմար» ճառագայթներն են.
ա) ոսպնյակի օպտիկական կենտրոնով անցնող ճառագայթը.
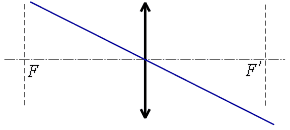
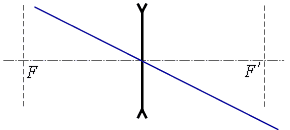
Ոսպնյակով անցնելիս այս ճառագայթը չի փոխում իր ուղղությունը:
բ) ոսպնյակի գլխավոր օպտիկական առանցքին զուգահեռ ճառագայթը.
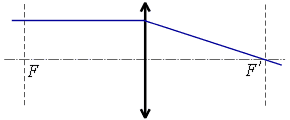
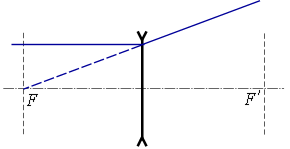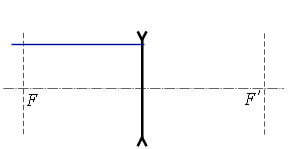
Ոսպնյակով անցնելիս, եթե ոսպնյակը հավքող է՝ ապա ճառագայթը, իսկ եթե ցրող է՝ ճառագայթի շարունակությունը, անցնում է ոսպնյակի գլխավոր կիզակետով:
Օգտվելով այս «հարմար» ճառագայթներից, օրինակ, կարող ենք կառուցել \(AB\) մատիտի պատկերը, եթե ստանանք նրա \(A\) և \(B\) ծայրակետերի պատկերները՝ -ը և -ը: հատվածը կլինի \(AB\) մատիտի պատկերը:
Կարելի է ցույց տալ, որ կախված առարկայի բարակ ոսպնյակից ունեցած հեռավորությունից, նրա պատկերը տարբեր է ստացվում:
Նշանակենք առարկայի հեռավորությունը բարակ ոսպնյակից՝ \(d\)-ով, նրա պատկերի հեռավորությունը ոսպնյակից՝ \(f\)-ով, իսկ ոսպնյակի կիզակետային հեռավորությունը՝ \(F\)-ով և դիտարկենք հետևյալ դեպքերը.
1. \(d >> F\) /առարկան շատ հեռու է ոսպնյակից/
Այս դեպքում առարկայից դուրս եկող ճառագայթները զուգահեռ կլինեն գլխավոր օպտիկական առանցքին, և առարկայի պատկերը կստացվի գլխավոր կիզակետում՝ լուսավոր փոքր կետի տեսքով:

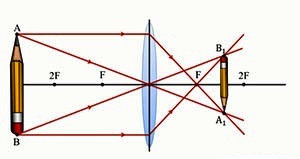
2. \(d >2F\) /առարկայի հեռավորությունը ոսպնյակից նրա կրկնակի կիզակետային հեռավորությունից մեծ է/
Օգտվելով «հարմար» ճառագայթներից կարող ենք կառուցել գլխավոր օպտիկական առանցքին ուղղահայաց տեղադրված \(AB\) սլաքի պատկերը՝ -ը: Ինչպես երևում է գծագրից, այն իրական է, շրջված, փոքրացած՝ \(H< h\), ստացվում է ոսպնյակի կիզակետի և կրկնակի կիզակետի միջև, այսինքն՝ \(F < f < 2F\):
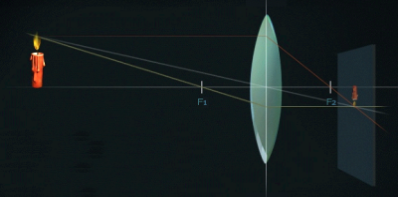
3. \(d = 2F\) /առարկան տեղադրված է ոսպնյակից՝ նրա կրկնակի կիզակետային հեռավորության վրա/
Կառուցումից երևում է, որ առարկայի պատկերը իրական է, շրջված, նույն չափերի՝ \(H = h\) և ոսպնյակից նույն հեռավորության վրա՝ \(d = 2F\):
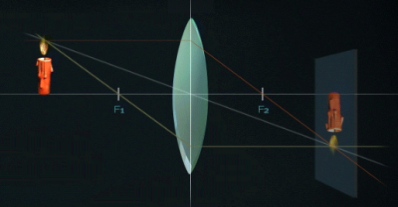
4. \(F < d < 2F\) /առարկան տեղադրված է ոսպնյակի կիզակետի և կրկնակի կիզակետի միջև/
Կառուցումից երևում է, որ սլաքի պատկերը իրական է, շրջված, մեծացած՝ \(H > h\) և ոսպնյակի կրկնակի կիզակետային հեռավորությունից մեծ հեռավորության վրա՝ \(f > 2F\)
\( \)

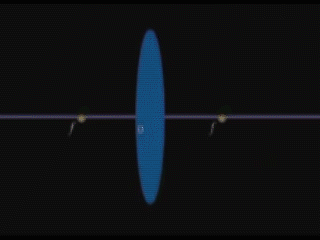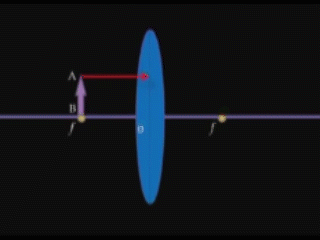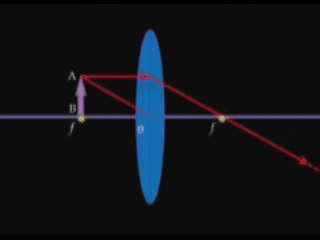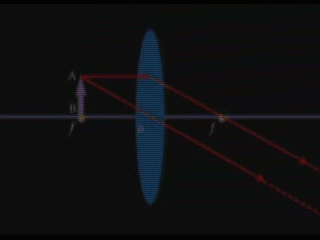
5. \(d = F\) /առարկան տեղադրված է ոսպնյակի գլխավոր կիզակետում/
Կառուցումից երևում է, որ սլաքի ծայրակետերից դուրս եկող ճառագայթները ոսպնյակում բեկվելուց հետո դառնում են իրար զուգահեռ, հետևաբար չեն հատվում և պատկեր չի ստացվում:
6. \(0 < d < F\) /առարկան տեղադրված է ոսպնյակի և նրա կիզակետի միջև/
Կառուցումից երևում է, որ սլաքի պատկերը ստացվում է կեղծ, ուղիղ, մեծացած՝ \(H > h\), ոսպնյակի նույն կողմում, որտեղ առարկան է:

Կատարելով նույնանման կառուցումներ, կստանանք, որ առարկայի պատկերը ցրող ոսպնյակում` անկախ առարկայի դիրքից, կեղծ է, փոքրացած, ուղիղ և ոսպնյակի նույն կողմում, որտեղ առարկան է:

Բարակ ոսպնյակի բանաձևը
Կառուցման եղանակով, օգտվելով ստացված եռանկյունների նմանության հայտանիշներից, կարելի է ցույց տալ, որ առարկայի հեռավորությունը ոսպնյակից՝ \(d\) -ն, առարկայի պատկերի հեռավորությունը ոսպնյակից՝ \(f\)-ը և ոսպնյակի կիզակետային հեռավորությունը` \(F\)-ը կապված են հավասարմամբ, որն անվանում են բարակ ոսպնյակի բանաձև:
Եթե ոսպնյակը հավաքող է, ապա բանաձևում \(F > 0\), իսկ եթե ցրող է, ապա \(F < 0\)
Եթե առարկայի պատկերը իրական է, ապա \(f > 0\), իսկ եթե կեղծ է, ապա \(f < 0\):
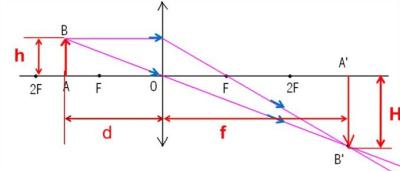
Կառուցման եղանակով, ստացված եռանկյունների նմանությունից հետևում է, որ
Իսկ ինչպես գիտենք, ոսպնյակի գծային խոշորացումը՝
Հետևաբար գծային խոշորացումը կարելի է որոշել նաև բանաձևով:
Աղբյուրները
Ֆիզիկա և աստղագիտություն 9; Է. Ղազարյան, Ա. Կիրակոսյան, Գ. Մելիքյան, Ռ. Թոսունյան, Ս. Մաիլյան, Ս. Ներսիսյան; Երևան 2009թ
Ֆիզիկա 9; Ս. Գրոմով, Ն. Ռոդինա, խմբագրությամբ Ա. Մամյանի,; Երևան 2015թ.
Ֆիզիկա 9; Ս. Գրոմով, Ն. Ռոդինա, խմբագրությամբ Ա. Մամյանի,; Երևան 2015թ.