
















Մաթեմատիկական և զսպանակավոր ճոճանակներ
Մաթեմատիկական ճոճանակը (թելավոր) բաղկացած է \(l\) երկարությամբ բարակ, թեթև թելից, որից կախված է \(m\) զանգվածով գնդիկ։
Այն պատկերված է նկարում։ Եթե գնդիկը, հավասարակշռության դիրքից հանելով, մի կողմ շեղենք ու բաց թողնենք, այն կսկսի տատանվել, այսինքն կրկնվող շարժումներ կատարել` պարբերաբար անցնելով հավասարակշռության դիրքով։
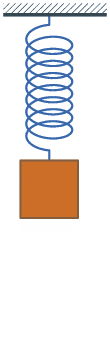
Տատանողական շարժումը բնութագրում են \(A\) լայնույթով, \(T\) պարբերությամբ և հաճախությամբ:
Այն տատանումները, որոնք կատարվում են համակարգում գործող ներքին ուժերի շնորհիվ, անվանում են ազատ տատանումներ::
Ուշադրություն
Մաթեմատիկական և զսպանակավոր և թելավոր ճոճանակների տատանումներն ազատ են:
Եթե ներքին ուժերի թվում կան նաև շփման կամ դիմադրության ուժեր, ապա տատանումների լայնույթն աստիճանաբար փոքրանում է:
Ազատ տատանումները կարող են տեղի ունենալ միայն որոշակի հաճախություններով և պարբերություններով, որոնք կախված են տատանողական համակարգի բնութագրիչներից:
Օրինակ
Զսպանակավոր ճոճանակը բնութագրվում է \(m\) զանգվածով և զսպանակի \(k\) կոշտությամբ, որոնցով էլ որոշվում է զսպանակից կախված բեռի ազատ տատանումների պարբերությունը՝
Մաթեմատիկական ճոճանակի ազատ տատանումների պարբերությունը կախված է թելի \(l\) երկարությունից և ազատ անկման \(g\) արագացումից՝
Մաթեմատիկական ճոճանակի տատանումների պարբերությունը կախված չէ մարմնի զանգվածից:
Իմանալով տատանումների պարբերությունը` կարելի է գտնել ազատ տատանումների հաճախությունը: Այն կոչվում է տատանողական համակարգի սեփական հաճախություն: Այս անվանումը պայմանավորված է նրանով, որ տատանողական յուրաքանչյուր համակարգ ունի իր բնութագրիչները, և առանց դրանք փոխելու անհնար է փոխել սեփական հաճախությունը::
Ազատ տատանումները ժամանակի ընթացքում մարում են: Այդ պատճառով գործնական նպատակներով ավելի հաճախ օգտագործում են ոչ թե ազատ, այլ հարկադրական տատանումները: Առավել լայնորեն դրանք կիրառվում են զանազան վիբրացիոն մեքենաներում:
Ռեզոնանս
Հարկադրական տատանումների տարբերիչ առանձնահատկությունը դրանց \(A\) լայնույթի կախվածությունն է արտաքին ուժի փոփոխման
հաճախությունից: Այս կախվածությունն ուսումնասիրելու համար կարելի է օգտվել նկարում պատկերված սարքից: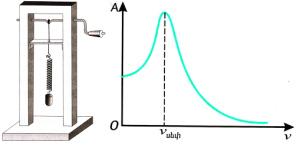 շ
շ= դեպքում հարկադրական տատանումների լայնույթի կտրուկ աճը կոչվում է ռեզոնանս:
Հարկադրական տատանումների լայնույթի՝ արտաքին ուժի փոփոխության հաճախությունից կախվածության գրաֆիկն անվանում են ռեզոնանսային կոր ( նկարում):
Այս կորի առավելագույն կետը համապատասխանում է այն հաճախությանը, որը հավասար է տատանումների սեփական հաճախությանը:
Ռեզոնանսի երևույթը կարելի է ցուցադրել նաև մաթեմատիկական ճոճանակների միջոցով: Փայտե ձողից կախենք մի մեծ գունդ (1) և մի քանի թեթև, տարբեր երկարության թելեր ունեցող ճոճանակներ (տե՛ս նկարը):
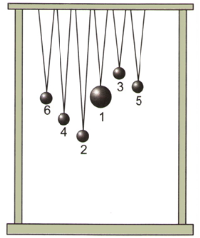
Ձեռք չտալով թեթև ճոճանակներին` հավասարակշռության վիճակից հանենք մեծ գունդը և բաց թողնենք: Ծանր գնդի ճոճվելու պատճառով ձողը կսկսի պարբերաբար ճկվել, ինչն էլ կհանգեցնի նրան, որ թեթև ճոճանակներից յուրաքանչյուրի վրա կսկսի ազդել պարբերաբար փոփոխվող առաձգականության ուժը: Դրա փոփոխման հաճախությունը հավասար կլինի գնդի տատանումների հաճախությանը:
Այս ուժի ներգործության հետևանքով ճոճանակները կսկսեն հարկադրական տատանումներ կատարել: Ընդ որում, մենք կտեսնենք, որ \(2\) և \(3\) ճոճանակները գրեթե անշարժ կմնան, \(4\) և \(5\)–ը կսկսեն տատանվել մի փոքր ավելի մեծ լայնույթով, իսկ \(6\)–ը, որն ունի թելի նույն երկարությունը, հետևաբար և տատանումների նույն սեփական հաճախությունը, ինչ–որ մեծ գունդը, կտատանվի ամենամեծ լայնույթով:


Ուշադրություն
Ռեզոնանսի երևույթը կարող է և՛ դրական, և՛ բացասական դեր խաղալ:
Հայտնի է, օրինակ, որ մեծ զանգի ծանր լեզվակը կարող է տարուբերել անգամ երեխան, եթե նա պարանի վրա ազդի լեզվակի ազատ տատանումներին համապատասխան:
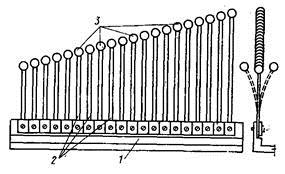
Ռեզոնանսի կիրառման վրա է հիմնված լեզվակավոր հաճախաչափի աշխատանքը: Այս սարքը ընդհանուր հիմքի վրա \((1)\) ամրացված տարբեր երկարության առաձգական թիթեղների \((2)\) և դրանց ամրացված փոքրիկ բեռների \((3)\) հավաքածու է: Ամեն մի թիթեղի սեփական հաճախությունը հայտնի է: Տատանողական համակարգի հետ, որի հաճախությունը պետք է որոշել, հաճախաչափի շփման ժամանակ առավելագույն լայնույթով սկսում է տատանվել այն թիթեղը, որի հաճախությունը համընկնում է չափվող հաճախությանը: Տեսնելով, թե որ թիթեղն է մտել ռեզոնանսի մեջ` մենք կորոշենք համակարգի տատանումների հաճախությունը (տե՛ս նկարը):
Ուշադրություն
Ռեզոնանսի կարող ենք հանդիպել նաև այնպիսի դեպքերում, երբ այն միանգամայն անցանկալի է:
Օրինակ
Այսպես, \(1750\) թվականին Ֆրանսիայի Անժեր քաղաքի մոտակայքում` \(102\) մ երկարությամբ շղթայակապ կամրջի վրայով, անցնում էր համաչափ քայլող զինվորների ջոկատը: Նրանց քայլերի հաճախությունը համընկավ կամրջի ազատ տատանումների հաճախությանը: Այդ պատճառով կամրջի տատանումների լայնույթը կտրուկ մեծացավ (սկսվեց ռեզոնանսը), և շղթաները պոկվեցին: Կամուրջն ընկավ գետը:Կարելի է հիշել նման այլ դեպքեր: Այժմ այդպիսի պատահարները կանխելու նպատակով կամրջով անցնելիս զորամասերին հրաման է տրվում շարժվել ոչ թե շարային, այլ ազատ քայլքով:
Իսկ եթե կամրջով գնացք է անցնում, ապա ռեզոնանսից խուսափելու համար այն կամ դանդաղ է շարժվում, կամ ընդհակառակն, առավելագույն արագությամբ:
Օրինակ
Ռեզոնանսի կարելի է հանդիպել ոչ միայն ցամաքում, այլև ջրում և անգամ օդում: Այսպես, թիալիսեռի պտտման որոշակի հաճախության դեպքում ռեզոնանսի մեջ են մտնում ամբողջական նավեր: Իսկ ավիացիայի զարգացման սկզբնական շրջանում որոշ շարժիչներ օդանավերի մասերի այնպիսի հուժկու ռեզոնանսային տատանումներ էին առաջացնում, որ օդանավերը կործանվում էին օդում:
Աղբյուրները
Ս. Վ. Գրոմով , Ն. Ա. Ռոդինա, Ֆիզիկա-8, հանրակրթական դպրոցի դասագիրք ( I, II, III և V գլուխների հեղինակ Ա. Մամյան); Երևան, Անտարես -2014 թ.