
















Հավասարաչափ շարժում շրջանագծով: Պտտման պարբերություն և հաճախություն
Կորագիծ շարժումը, որի դեպքում մարմնի հետագիծը շրջանագիծ է, կոչվում է շրջանագծային շարժում:
 |  |  |
Ուղղագիծ շարժումները ժամանակի մեջ սահմանափակ են: Մինչդեռ շրջանագծային շարժումներն ինչքան ասես երկար կարող են տևել: Օրինակ՝ ժամացույցի սլաքների կետերը շարժվում են շրջանագծով նրա ողջ գոյության ընթացքում:
Ուշադրություն
Շրջանագծային շարժումն ունի ևս մեկ առանձնահատկություն, որով օժտված չեն ուղղագիծ շարժումները: Դա նրա պարբերականությունն է:
Պարբերական նշանակում է ժամանակի ընթացքում կրկնվող, իսկ այն ժամանակամիջոցը, որից հետո կրկնվում է տվյալ երևույթը, անվանում են պարբերություն:
Մարմինը շարժվում է հավասարաչափ, նշանակում է նրա արագության մեծությունը հաստատուն է (\(v – cօnst\)), ուստի \(t\) ժամանակում նրա անցած ճանապարհը որոշվում է \(S = vt\) բանաձևով.
Ուշադրություն
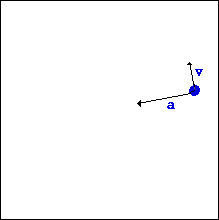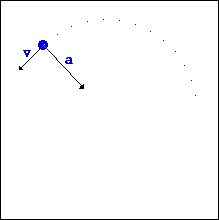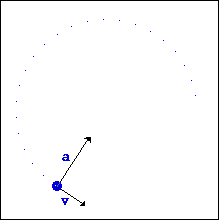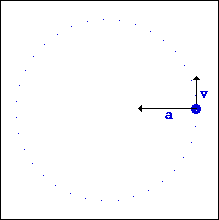
Ինչպես կամայական կորագիծ շարժման ժամանակ, այնպես էլ շրջանագծային շարժման դեպքում մարմնի ակնթարթային արագության ուղղությունը անընդհատ փոփոխվում է: Փորձը ցույց է տալիս, որ հետագծի յուրաքանչյուր կետում արագությունն ուղղված է այդ կետում հետագծին տարված շոշափողով:
Օրինակ
Ջրափոսում ավտոմեքենայի տեղապտույտ տվող անիվից պոկված ջրի կաթիլները անիվից պոկվելու կետում թռչում են նրա եզրագծին տարված շոշափողով: Սղոցով մետաղ կտրելիս արձակվող կայծերի հետագծերն էլ են նույնը՝ պոկվելու կետում շոշափողի ուղղությամբ (տե՛ս նկարները):

Ուշադրություն
Շրջանագծային շարժումն ունի ևս մեկ առանձնահատկություն, որով օժտված չեն ուղղագիծ շարժումները: Դա նրա պարբերականությունն է:
Դիցուք որևէ պահի մարմինը գտնվում է հետագծի \(A\) կետում և ունի \(v\) արագություն: Մեկ պտույտ կատարելուց հետո այն կրկին \(A\) կետում կլինի և դարձյալ կունենա \(v\) արագություն:
Եթե մեկ պտույտ կատարելու ժամանակամիջոցը նշանակենք \(T\) տառով, ապա կստացվի, որ մարմնի շարժումը նույնությամբ կրկնվում է` մասնավորապես յուրաքանչյուր \(T\) ժամանակամիջոցից հետո:
Պարբերական շարժումները բնութագրվում են պարբերությամբ և հաճախությամբ:
Շրջանագծային հավասարաչափ շարժման պտտման պարբերություն
Այն ժամանակամիջոցը, որի ընթացքում շրջանագծային հավասարաչափ շարժում կատարող մարմինը կատարում է մեկ լրիվ պտույտ, կոչվում է պտտման պարբերություն:
Համաձայն սահմանման՝ պտտման պարբերությունը ժամանակամիջոց է, հետևաբար նրա չափման միավորը ՄՀ-ում \(1\) վայրկյանն է (\(1\) վ):
Այսպիսով, պտտման պարբերությունը որոշելու համար անհրաժեշտ է \(N\) թվով պտույտներ կատարելու վրա ծախսված ժամանակը բաժանել պտույտների թվի վրա.
Եթե հայտնի է պտտման \(T\) պարբերությունը և շրջանագծի \(r\) շառավիղը, ապա կարելի է որոշել մարմնի \(v\) արագությունը: Իրոք, \(T\) ժամանակում մարմինն անցնում է շրջանագծի երկարությանը հավասար՝ ճանապարհ, որտեղ
Քանի որ շարժումը հավասարաչափ է, ապա մարմնի արագությունը՝
Շրջանագծային հավասարաչափ շարժման պտտման հաճախություն
Ուշադրություն
Շրջանագծային հավասարաչափ շարժումը հարմար է բնութագրել պարբերությամբ այն դեպքերում, երբ պտտման պարբերությունը մեծ է ժամանակի
միավորից:
Ուշադրություն
Երբ պտտման պարբերությունը փոքր է ժամանակի միավորից, շրջանագծային հավասարաչափ շարժումը հարմար է բնութագրել պտտման հաճախությամբ` \(n\):
Շրջանագծային հավասարաչափ շարժման պտտման հաճախություն կոչվում է կամայական ժամանակամիջոցում մարմնի կատարած պտույտների \(N\) թվի և պարբերության հակադարձ մեծությունը:
Աղբյուրները
Ս. Վ. Գրոմով , Ն. Ա. Ռոդինա, Ֆիզիկա-8, հանրակրթական դպրոցի դասագիրք ( I, II, III և V գլուխների հեղինակ Ա. Մամյան); Երևան, Անտարես -2014 թ.