
















Ազատ անկում: Ազատ անկման արագացում
Մարմինների անկումը, որը տեղի է ունենում միայն Երկրի ձգողության ազդեցությամբ, կոչվում է ազատ անկում:

Իտալացի գիտնական Գալիլեո Գալիլեյը, ուսումնասիրելով Պիզա քաղաքում գտնվող թեք աշտարակից ընկնող մարմինների շարժումը, եզրակացրեց, որ բոլոր մարմինները Երկրի ձգողության ազդեցությամբ ընկնում են նույն արագացմամբ:

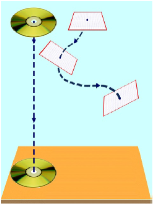
Թվում է, թե առօրյա դիտումները չեն հաստատում այդ օրենքը: Իրոք, սովորական պայմաններում տարբեր մարմիններ տարբեր կերպ են ընկնում: Լազերային սկավառակը, օրինակ, ընկնում է արագ, իսկ տետրի թերթի կտորը՝ դանդաղ և, բացի այդ, բարդ հետագծով (տե՛ս նկար):
Գալիլեյի օրենքի ճշմարտացիությունն ապացուցելու համար վերցնում են մոտ \(1\) մ երկարությամբ ապակե խողովակ, որը մի կողմից փակ է, իսկ մյուս կողմից ծորակ ունի, և որի մեջ դրված են կապարե գնդիկ, խցան և փետուր: Սկզբում խողովակը պահում են ուղղաձիգ դիրքով (տե՛ս նկար), հետո այն արագ շրջում են \(180°\)-ով:
Այնուհետև պոմպով օդը հանում են խողովակից և կրկին շրջում այն: Այս անգամ արդեն բոլոր երեք մարմինները ընկնում են միաժամանակ, ինչը և վկայում է, որ բոլոր մարմինները շարժվում են նույն արագացմամբ (տե՛ս նկար):
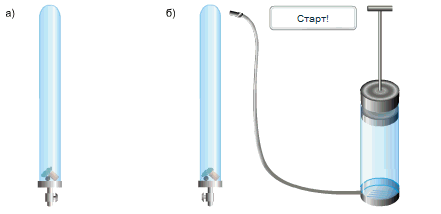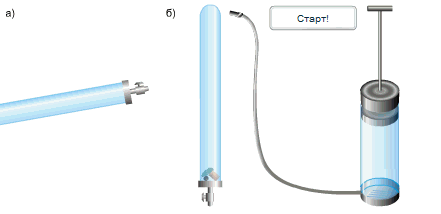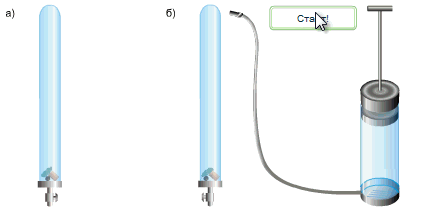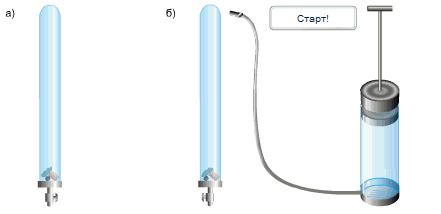
Ազատ անկման արագացումը
Համաձայն Գալիլեյի օրենքի՝ բոլոր մարմինները Երկրի ձգողության ազդեցությամբ ընկնում են նույն արագացմամբ:Ուշադրություն
Ազատ անկման արագացումը ընդունված է նշանակել \(g\) տառով: Բազմաթիվ փորձերի արդյունքում ստացվել է, որ Երկրի միջին լայնություններում ազատ անկման արագացումը՝ \(g = 9,8\) մ/վ²: Ազատ անկման արագացման վեկտորն ուղղված է ուղղաձիգ դեպի ներքև:
Դադարի վիճակից ազատ անկում կատարող մարմնի շարժումը
Դիցուք մարմինն ազատ անկում է կատարում \(H\) բարձրությունից: Որոշենք անկման սկզբից \(t\) ժամանակ անց նրա արագությունը, անցած ճանապարհը և գետնից ունեցած բարձրությունը:Տվյալ դեպքում մարմնի շարժումը դադարի վիճակից հավասարաչափ արագացող է, հետևաբար նրա արագությունը և անցած ճանապարհը կարելի է որոշել հավասարաչափ արագացմամբ շարժվող բանաձևերով՝ , դրանց մեջ \(a\)-ն փոխարինելով \(g\)-ով. ,
Ինչպես երևում է նկարից, ժամանակի \(t\) պահին մարմնի բարձրությունը գետնից հավասար է նրա սկզբնական բարձրության և անցած ճանապարհի տարբերությանը:
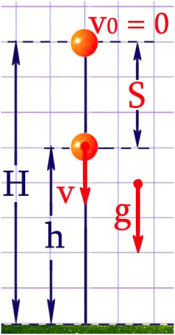
Այժմ պարզենք, թե որքան ժամանակում մարմինը կհասնի գետնին, և ինչ արագություն կունենա գետնին հարվածելու պահին:
Գետնին հարվածելու պահին \(S = H\) (կամ որ նույնն է \(h = 0\)): Հետևաբար վերը նշված հավասարումից կստանանք, որ վայրէջքի ժամանակը՝
-ի արժեքը տեղադրելով արագության բանաձևի մեջ՝ կստանանք մարմնի արագությունը գետնին հասնելու պահին.
Ուղղաձիգ դեպի վեր նետած մարմնի շարժումը
սկզբնական արագությամբ ուղղաձիգ դեպի վեր նետած մարմնի շարժման դեպքում (տե՛ս նկարը) մարմնի արագացումն ուղղված է շարժման հակառակ ուղղությամբ, հետևաբար այն հավասարաչափ դանդաղող է: Մարմնի արագությունն աստիճանաբար նվազում է և հետագծի ամենաբարձր կետում դառնում զրո:
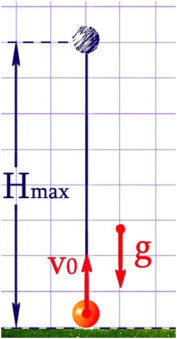
Հետևաբար, դանդաղող շարժման արագության \(v = v0 – at\) բանաձևում տեղադրելով \(v = 0\) և \(a = g\), կստանանք. \(0 =\) – \(g\), որտեղ -ը վերելքի ժամանակն է: Այսպիսով՝
Վերելքի առավելագույն բարձրությունը կարող ենք գտնել՝ բանաձևում տեղադրելով \(t =\) և \(a = g\)
Վերելքի առավելագույն բարձրությունը կարող ենք գտնել՝ բանաձևում տեղադրելով \(t =\) և \(a = g\)
Աղբյուրները
Գրոմով Ս.Վ., Ռոդինա Ն. Ա., խմբագրությամբ՝ Ա. Լ. Մամյանի; Դասագիրք հանրակրթական հաստատությունների 8-րդ դասարանի համար - Եր.։ Անտարես, 2013թ.