Մեխանիկական էներգիայի փոխակերպումը մի տեսակից մյուսին,մեխ. էներգիայի պահպանման օրենքը

Լրիվ մեխանիկական էներգիա

Մարմինը միաժամանակ կարող է ունենալ և՛ կինետիկ, և՛ պոտենցիալ էներգիա։

\(h\) բարձրության վրա արագությամբ շարժվող մարմնի լրիվ մեխանիկական էներգիան՝

E_{լր} = \frac{m v^{2}}{2} + mgh

Մեխանիկական էներգիայի փոխակերպումը մի տեսակից մյուսին

Գնդիկին \(A\) կետում

v_{0}

արագություն հաղորդելով` մենք նրան

E_{կ} = \frac{m v^{2}}{2}

կինետիկ էներգիա ենք հաղորդում (տե՛ս նկար)։ Եթե զրոյական մակարդակ ընդունենք \(A\) մակարդակը, ապա գնդիկի պոտենցիալ էներգիան սկզբում զրո կլինի: Վերև բարձրանալիս գնդիկի արագությունն աստիճանաբար նվազում է, իսկ զրոյական մակարդակից ունեցած բարձրությունը՝ աճում: Դա նշանակում է, որ նրա կինետիկ էներգիան աստիճանաբար փոխակերպվում է պոտենցիալ էներգիայի: Հետագծի ամենաբարձր`\(C\) կետում գնդակի կինետիկ էներգիան դառնում է զրո, իսկ պոտենցիալ էներգիան հասնում է իր առավելագույն արժեքին՝

E_{պ} = mg H_{առ .}

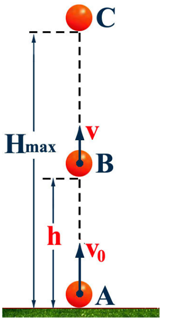
Դրանից հետո գնդիկը սկսում է ցած ընկնել՝ աստիճանաբար մեծացնելով արագությունը: Վայրէջքի ընթացքում տեղի է ունենում հակառակ պրոցեսը՝ գնդիկի պոտենցիալ էներգիան փոխակերպվում է կինետիկ էներգիայի:

Ուշադրություն

Այսպիսով, շարժման ընթացքում անընդհատ տեղի է ունենում կինետիկ էներգիայի փոխակերպում պոտենցիալ էներգիայի և հակառակը: Ընդ որում, երբ մի տեսակի էներգիան նվազում է, մյուս տեսակի էներգիան աճում է:

Լրիվ մեխանիկական էներգիայի վարքը ազատ անկման դեպքում

Իսկ ի՞նչ է տեղի ունենում գնդիկի լրիվ մեխանիկական էներգիայի հետ:

Հաշվենք մարմնի լրիվ մեխանիկական էներգիան վերելքի կամայական \(B\) կետում: Այդ կետի \(հ\) բարձրությունը մարմնի անցած ճանապարհն է՝

h = \frac{v_{0} + v}{2} t

, որտեղ \(t\)-ն \(AB\) տեղամասն անցնելու ժամանակն է:

Մարմնի արագությունը՝

v = v_{0} - gt

, այսինքն՝

t = \frac{v - v_{0}}{g}

Տեղադրելով \(t\)-ի արտահայտությունը \(h\)-ի հավասարման մեջ, կստանանք՝

\begin{array}{l} h = \frac{v_{0} + v}{2} \cdot \frac{v_{0} - v}{g} = \frac{(v_{0} + v) \cdot (v_{0} - v)}{2 g} = \frac{v_{0}^{2} - v^{2}}{2 g}; այսինքն \\ h = \frac{v_{0}^{2} - v^{2}}{2 g} \end{array}

Այսինքն՝ լրիվ մեխանիկական էներգիան \(B\) կետում կլինի.

E_{B} = \frac{m v^{2}}{2} + mg \cdot \frac{v_{0}^{2} - v^{2}}{2 g} = \frac{m v^{2}}{2} + \frac{m v_{0}^{2}}{2} - \frac{m v^{2}}{2} = \frac{m v_{0}^{2}}{2} = E_{A}

Այստեղ

E_{B}

–ն գնդիկի լրիվ մեխանիկական էներգիան է \(B\) կետում, իսկ

E_{A}

-ն՝ \(A\) կետում (շարժման սկզբում): Հաշվի առնելով, որ \(B\) կետն ընտրված էր կամայականորեն, ուրեմն, չնայած շարժման ընթացքում մարմնի կինետիկ և պոտենցիալ էներգիաները փոփոխվում են, սակայն դրանց գումարը մնում է հաստատուն, այսինքն՝ լրիվ մեխանիկական էներգիան պահպանվում է:

Լրիվ մեխանիկական էներգիայի պահպանման օրենքը

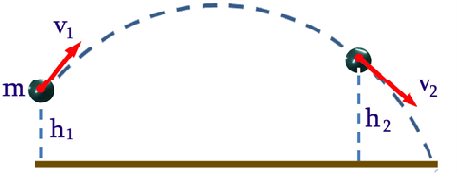
Լրիվ մեխանիկական էներգիան հորիզոնի նկատմամբ անկյան տակ նետած մարմնի շարժման դեպքում էլ է պահպանվում: Եթե անկյան տակ նետած մարմնի արագությունը

h_{1}

բարձրության վրա

v_{1}

է, իսկ

h_{2}

բարձրության վրա՝

v_{2}

, ապա

\frac{m_{1} v_{1}^{2}}{2} + mg h_{1} = \frac{m_{2} v_{2}^{2}}{2} + mg h_{2}

Ուշադրություն

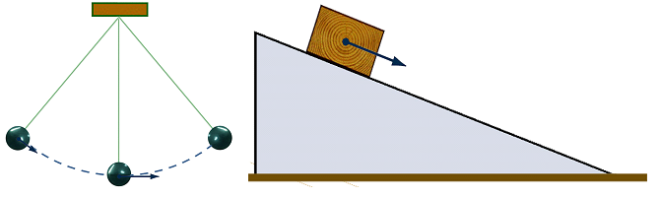
Բայց մարմնի լրիվ մեխանիկական էներգիան պահպանվում է ոչ միայն ազատ անկման դեպքում: Փորձը ցույց է տալիս, որ այն պահպանվում է բոլոր այն դեպքերում, երբ շարժումը տեղի է ունենում օդի դիմադրության և շփման ուժերի բացակայության պայմաններում: Այդպիսի շարժումների օրինակներն են նաև թելից կախված գնդիկի և թեք հարթությամբ սահող մարմնի շարժումները, եթե դիմադրության և շփման ուժերը կարելի է անտեսել (տե՛ս նկար):

Ընդհանրացնելով մեր քննարկած, ինչպես նաև բազմաթիվ այլ փորձերի արդյունքները՝ կարող ենք ձևակերպել մեխանիկական էներգիայի պահպանման օրենքը.

Դիմադրության և շփման ուժերի բացակայության պայմաններում մարմնի լրիվ մեխանիկական էներգիան պահպանվում է:

Ուշադրություն

Դիմադրության և շփման ուժերի առկայության դեպքում մարմնի լրիվ մեխանիկական էներգիան չի պահպանվում: Այդ ուժերի ազդեցության հետևանքով մարմինն աստիճանաբար կորցնում է իր մեխանիկական էներգիան: Իհարկե, դա չի նշանակում, որ էներգիան ընդհանրապես կորչում է: Պարզապես մեխանիկական էներգիան փոխակերպվում է էներգիայի այլ տեսակների, որոնց մենք կծանոթանանք հետագայում:

Շարժվող ջրի և քամու էներգիայի օգտագործումը

Ջուրը կարող է օժտված լինել ինչպես կինետիկ, այնպես էլ պոտենցիալ էներգիայով։ Ամբարտակի միջոցով գետի ջրի մակարդակը բարձրացնելով` մեծացնում ենք ջրի պոտենցիալ էներգիան։

Շարժվող ջրի կինետիկ էներգիան օգտագործում են ջրային տուրբինի պտուտակները շարժման մեջ դնելու համար։
Կինետիկ էներգիայով օժտված է նաև շարժվող օդը` քամին։ Նրա էներգիան օգտագործվում է հողմաշարժիչներում։ Հայաստանում \(2.6\) ՄՎտ հզորությամբ առաջին հողմաէլեկտրակայանը (տե՛ս նկար) գործարկվել է Պուշկինի լեռնանցքի տարածքում (Վանաձորի և Ստեփանավանի միջև) \(2005\) թ:

Երկրորդ՝ Շիրակի հողմաէլեկտրակայանի (տե՛ս նկար) հզորությունը \(90\) ՄՎտ է:

Միջին դարերում լայնորեն տարածված էին հողմաղացները։

Քամու ժամանակակից շարժիչներում հաջողվում է կարգավորել նույնիսկ հողմապտուտակի պտույտների հաճախությունը։ Երբ քամին ուժեղանում է, հողմաթևերը շրջվում են` եզրերը դարձնելով դեպի քամին, երբ քամին թուլանում է, շրջվում են` ճակատը դարձնելով դեպի քամին։

Քամու էներգիա արտադրող կայանները ներդաշնակորեն համադրվում են շրջակա միջավայրի հետ։

Ի տարբերություն ջերմային ու ատոմային էլեկտրակայանների` քամու կայանները կառուցումից հետո վառելիքի ծախս չեն պահանջում և էկոլոգիապես մաքուր են։
Էկոլոգիապես մաքուր են նաև մակընթացային էլեկտրակայանները (ՄԷԿ-երը), որոնք օգտագործում են ծովերի ու օվկիանոսների ջրի մակընթացությունն ու տեղատվությունը։

Աղբյուրները

Ս. Վ. Գրոմով , Ն. Ա. Ռոդինա, Ֆիզիկա-8, հանրակրթական դպրոցի դասագիրք ( I, II, III և V գլուխների հեղինակ Ա. Մամյան); Երևան, Անտարես -2014 թ.

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Մեխանիկական էներգիայի փոխակերպումը մի տեսակից մյուսին,մեխ. էներգիայի պահպանման օրենքը

Տեսություն