Վեկտորի վերածումն՝ ըստ տարագիծ վեկտորների զույգի

Հիշենք, որ վեկտորը

k \neq 0

թվով բազմապատկելիս ստանում ենք երկու համագիծ վեկտորներ, ընդ որում, եթե

k > 0

, ապա վեկտորները համուղղված են, իսկ եթե

k < 0

, ապա վեկտորները հակուղղված են: Վեկտորների երկարությունները տարբերվում են \(k\) անգամ:

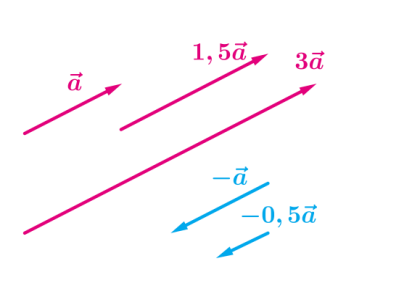
Ճիշտ է նաև հակադարձ պնդումը:

Եթե

\vec{a}

\vec{b}

ոչ զրոյական վեկտորները համագիծ են, ապա գոյություն ունի

k \neq 0

թիվ այնպիսին

\vec{b} = k \cdot \vec{a}

Հիմա դիտարկենք

\vec{a}

\vec{b}

ոչ համագիծ (տարագիծ) վեկտորները:

Ասում են, որ

\vec{c}

վեկտորը վերածվում է ըստ

\vec{a}

\vec{b}

տարագիծ վեկտորների, եթե գոյություն ունեն \(k\) և \(m\) թվեր այնպիսին, որ

\vec{c} = k \cdot \vec{a} + m \cdot \vec{b}

\(k\) և \(m\) թվերը կոչվում են վերածման գործակիցներ:

Ցանկացած վեկտոր կարելի է վերածել ըստ տրված երկու տարագիծ վեկտորների, ընդ որում՝ գործակիցները որոշվում են միակ ձևով:

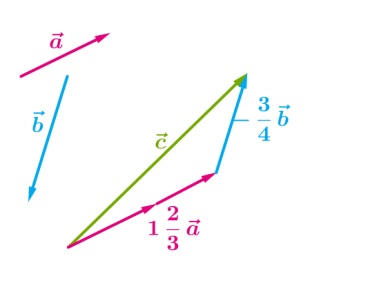
Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, "Զանգակ", 2013:

Սխա՞լ ես գտել

1. Վեկտորի վերածումն՝ ըստ տարագիծ վեկտորների զույգի