
















Վեկտորի տեղադրումը տրված կետից
Հիշենք վեկտորների հավասարության սահմանումը:
Վեկտորները կոչվում են հավասար, եթե նրանք համուղղված են, և նրանց երկարությունները հավասար են:
Սահմանումից երևում է, որ վեկտորների հավասարությունը կախված է վեկտորների երկարություններից և ուղղություններից, իսկ սկզբնակետերն ու վերջնակետերը դեր չեն խաղում:
Մասնավորապես, եթե վեկտորների մոդուլները և ուղղությունները համընկնում են, ապա նրանց սկզբնակետերը կարող են ցանկացած կետեր լինել:
Եթե կետը վեկտորի սկիզբն է, ապա ասում են, որ վեկտորը տեղադրված է կետում:
Ցանկացած կետից կարելի է տեղադրել տրված վեկտորին հավասար միակ վեկտորը:
Տարբեր կետերից տեղադրված հավասար վեկտորները նշանակում են նույն տառով և չեն տարբերում իրարից:
Այդ դեդեպքում վեկտորի մոդուլն ու ուղղությունը որոշվում են միայն նրա վերջնակետի կոորդինատներով՝ (տես ներքևի նկարը):
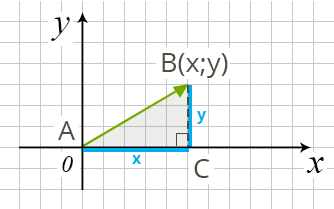
վեկտորի կոորդինատներ անվանում են վեկտորը կետում տեղադրելուց առաջացած վերջնակետի կոորդինատները և գրում՝
Եթե գտնված են վեկտորի կոորդինատները՝ , ապա շատ հարցեր հեշտանում են: Մասնավորապես, ըստ Պյութագորասի թեորեմի, գտնում ենք վեկտորի մոդուլը՝
Ուշադրություն
Այսպիսով, վեկտորի կոորդինատները գտնելու համար պետք է այն տեղադրել կետում և որոշել առաջացած վեկտորի վերջնակետի կոորդինատները:
Դիցուք տրված է սկզբնակետով և վերջնակետով վեկտորը:
Տեղադրենք վեկտորը կետում և որոշենք առաջացած վեկտորի վերջնակետի կոորդինատները:
Եթե նշանակենք և , ապա հենց այս թվերը կլինեն վեկտորի կոորդինատները՝
Այսպիսով՝ սկզբնակետով և վերջնակետով վեկտորի կոորդինատները հավասար են վերջնակետի և սկզբնակետի կոորդինատների տարբերություններին՝
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի.Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, "Զանգակ", 2013: