Եռանկյունների նմանության հայտանիշները — դաս։ Երկրաչափություն, 9-րդ դասարան.

Եռանկյունների նմանության առաջին հայտանիշը

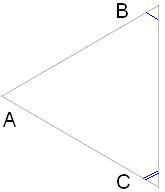
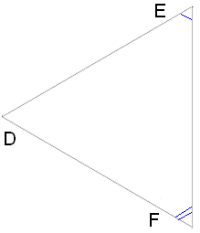
\(I\). Եթե մի եռանկյան երկու անկյունները համապատասխանաբար հավասար են մյուս եռանկյան երկու անկյուններին, ապա եռանկյունները նման են:

Եթե

∢

\(B =\)

∢

\(E\) և

∢

\(C =\)

∢

\(F\), ապա

Δ ABC \sim Δ DEF

Եռանկյունների նմանության երկրորդ հայտանիշը

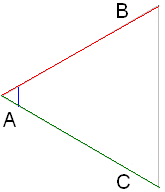
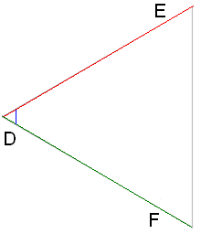
\(II.\) Եթե մի եռանկյան երկու կողմերը համեմատական են մյուս եռանկյան երկու կողմերին, իսկ այդ կողմերով կազմված անկյունները հավասար են, ապա եռանկյունները նման են:

Եթե

\frac{AB}{DE} = \frac{AC}{DF}

և

∢

\(A =\)

∢

\(D\), ապա

Δ ABC \sim Δ DEF

Եռանկյունների նմանության երրորդ հայտանիշը

\(III\). Եթե մի եռանկյան երեք կողմերը համեմատական են մյուս եռանկյան երեք կողմերին, ապա եռանկյունները նման են:

Եթե

\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}

, ապա

Δ ABC \sim Δ DEF

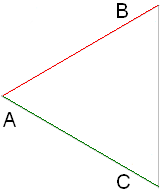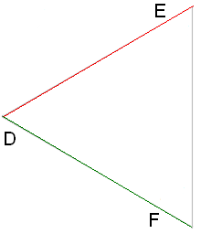Խնդիրներ լուծելիս, սկզբում պետք է համոզվել, որ տրված եռանկյունները նման են:

Եթե եռանկյունների նմանությունը տրված չէ, ապա դա պետք է ապացուցել:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, "Զանգակ", 2013:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ