2. Եռանկյան միջնագիծը

 

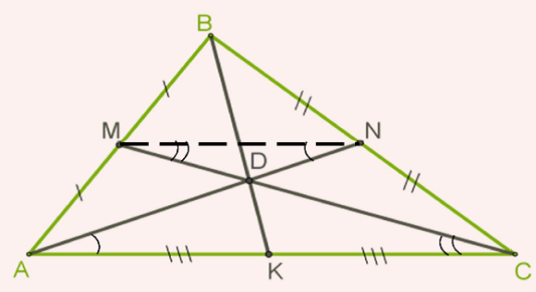
Դիտարկենք \(ABC\) եռանկյունը, \(D\)-ն \(CM\) և \(AN\) միջնագծերի հատման կետն է:

 

Տանենք \(ABC\) եռանկյան \(MN\) միջին գիծը: Քանի որ \(MN\)-ը զուգահեռ է \(AC\) կողմին, ուրեմն, $\measuredangle \mathit{NAC}=\measuredangle \mathit{ANM}\text{ և }\measuredangle \mathit{MCA}=\measuredangle \mathit{CMN}$, ապա \(ADC\) և \(MDN\) եռանկյունները նման են, ըստ երկու անկյան:

 

Հետևաբար, այդ եռանկյունների կողմերը համեմատական են՝

 

 

Քանի որ, ըստ \(MN\) միջին գծի հատկության \(AC = 2·MN\), ապա \(AD = 2·ND\) և \(CD = 2·MD\)

 

Այսպիսով, \(AN\) և \(CM\) միջնագծերից յուրաքանչյուրը հատման \(D\) կետով տրոհվում է \(2 : 1\) հարաբերությամբ՝ հաշված գագաթից:

 

Նույն կերպ ապացուցում ենք, որ \(CM\) և \(BK\) միջնագծերը հատվելիս տրոհվում են \(2 : 1\) հարաբերությամբ՝ հաշված գագաթից: Հետևաբար, դրանց հատման կետը համընկնում է \(D\) կետի հետ: