Գնդի ծավալը — դաս։ Երկրաչափություն, 9-րդ դասարան.

Գնդի ծավալը

Հիշենք, որ գլանի ծավալը հավասար է հիմքի մակերեսի և բարձրության արտադրյալին՝

V = S_{հիմք} \cdot h

Այս բանաձևի օգնությամբ ստանանք գնդի ծավալի հաշվման բանաձևը:

Բանաձևի իրական ապացույցը պահանջում է բավականին բարդ հաշվարկներ:

Բերենք մ.թ.ա. \(III\)-րդ դարում ապրած հույն գիտնական Արքիմեդի հայտնաբերած մի օրինաչափություն, որի միջոցով ստացվում է գնդի ծավալի բանաձևը:

Դիցուք՝ \(R\) շառավղով և \(2R\) բարձրությամբ գլանին ներգծված է \(R\) շառավղով գունդ:

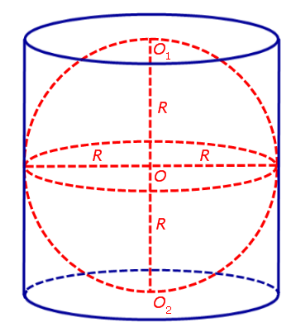
Պարզվում է, որ գնդի ծավալը (ինչպես և գնդի մակերևույթի մակերեսը) կազմում է գլանի ծավալի (լրիվ մակերևույթի մակերեսի)

\frac{2}{3}

-ը:

Քանի որ դիտարկվող գլանի ծավալը հավասար է՝

V_{գլան} = S_{հիմք} \cdot h = π R^{2} \cdot 2 R = 2 π R^{3}

, ապա դրա

\frac{2}{3}

-ը կլինի՝

V_{գունդ} = \frac{2}{3} \cdot V_{գլան} = \frac{2}{3} \cdot 2 π R^{3} = \frac{4}{3} \cdot π R^{3}

Այսպիսով, գնդի ծավալը հաշվվում է հետևյալ բանաձևով՝

V_{գունդ} = \frac{4}{3} \cdot π R^{3}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ», 2013

Սխա՞լ ես գտել

1. Գնդի ծավալը