
















Բուրգի ծավալը
Դիտարկենք \(a\) կողմով խորանարդ, որում տարված են նրա անկյունագծերը:
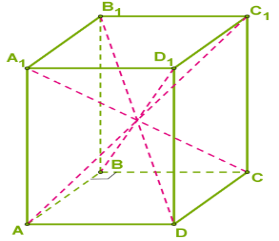
Արդյունքում խորանարդը տրոհվում է վեց հավասար կանոնավոր քառանկյուն բուրգերի, որոնց գագաթը անկյունագծերի հատման կետն է:
Քանի որ խորանարդի ծավալը հավասար է՝ , ապա բուրգերից յուրաքանչյուրի ծավալը կլինի
Հաշվի առնելով, որ բուրգերի հիմքերը խորանարդի նիստերն են՝ մակերեսով, իսկ բարձրությունները հավասար են խորանարդի կողի կեսին՝ , ձևափոխենք բուրգի ծավալի ստացած բանաձևը՝
Պարզվում է, որ ստացված բանաձևը ճիշտ է կամայական բուրգի համար:
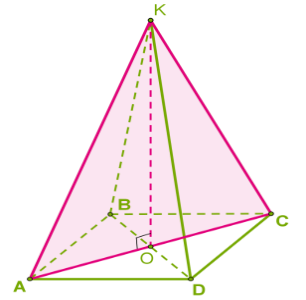
Բուրգի ծավալը հավասար է նրա հիմքի մակերեսի և բարձրության արտադրյալի երրորդ մասին՝
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ», 2013