Շրջանագծի հավասարումը — դաս։ Երկրաչափություն, 9-րդ դասարան.

Շրջանագծի հավասարումը

Դուրս բերենք տրված կենտրոնով և տրված շառավղով շրջանագծի հավասարումը:

1. Շրջանագծի բոլոր կետերը գտնվում են միևնույն կետից \((\)կենտրոն\()\) միևնույն հեռավորության վրա \((\)շառավիղ\()\):

2. Մենք ունենք երկու կետերի միջև հեռավորության հաշվման բանաձևը՝

|AB| = \sqrt{{(x_{A} - x_{B})}^{2} + {(y_{A} - y_{B})}^{2}}

Բարձրացնելով քառակուսի՝ ստանում ենք՝

{AB}^{2} = {(x_{A} - x_{B})}^{2} + {(y_{A} - y_{B})}^{2}

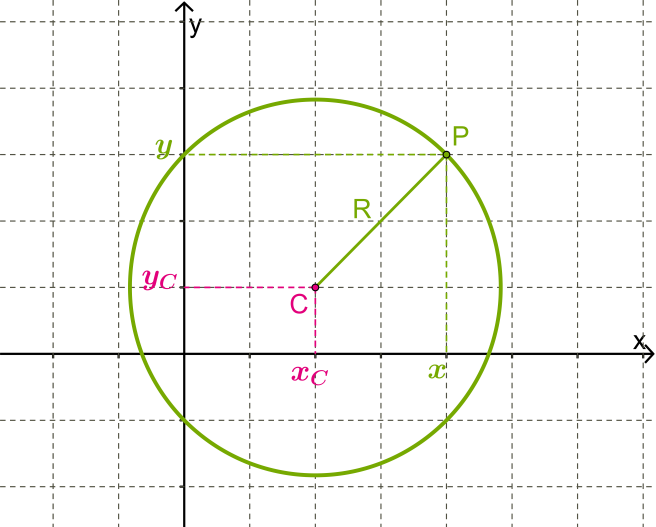
Դիցուք շրջանագծի կենտրոնը

C (x_{C}; y_{C})

կետն է, իսկ շառավիղը՝ \(R\)-ն է:

Շրջանագծի ցանկացած

P (x; y)

կետ գտնվում է \(C\) կենտրոնից \(R\) հեռավորության վրա:

Հետևաբար, տեղի ունի հետևյալ հավասարությունը՝

{(x - x_{C})}^{2} + {(y - y_{C})}^{2} = R^{2}

Սա հենց \(C\) կենտրոնով և \(R\) շառավղով շրջանագծի հավասարումն է:

Եթե շրջանագծի կենտրոնը կոորդինատների

(0; 0)

սկզբնակետն է, ապա հավասարումը ստանում է հետևյալ տեսքը՝

x^{2} + y^{2} = R^{2}

Օրինակ

Կազմենք այն շրջանագծի հավասարումը, որն անցնում է կոորդինատների սկզբնակետով, իսկ կենտրոնը

(- 3; 4)

կետն է:

Լուծում: Շրջանագծի կենտրոնը տրված է, ուրեմն, մնում է գտնել նրա շառավիղը:

Շրջանագիծն անցնում է

(0; 0)

կետով, ուրեմն, շառավիղը հավասար է հեռավորությանը

(- 3; 4)

(0; 0)

կետերի միջև:

Հաշվենք այն՝

d = \sqrt{{(- 3 - 0)}^{2} + {(4 - 0)}^{2}} = \sqrt{9 + 16} = 5

Այսպիսով, պահանջվող շրջանագծի կենտրոնը

(- 3; 4)

կետն է, իսկ շառավիղը՝

R = 5

Ըստ վերևում բերված բանաձևի, կազմում ենք շրջանագծի հավասարումը՝

{(x + 3)}^{2} + {(y - 4)}^{2} = 25

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, Զանգակ, 2013

Սխա՞լ ես գտել

1. Շրջանագծի հավասարումը