Խնդիրների լուծումը կոորդինատային եղանակով — դաս։ Երկրաչափություն, 9-րդ դասարան.

Կոորդինատային համակարգի ներմուծման միջոցով հնարավոր է դառնում շատ երկրաչափական խնդիրներ արտահայտել հանրահաշվի լեզվով, և լուծել դրանք հանրահաշվական թեորեմների և բանաձևերի կիրառմամբ:

Օրինակ

Խնդիր: Ապացուցեք, որ ուղղանկյուն եռանկյան ներքնաձիգի միջնակետը հավասարահեռ է նրա բոլոր գագաթներից:

Լուծում: Եռանկյունը կոորդինատային հարթության վրա տեղադրենք այնպես, որ նրա ուղիղ անկյան գագաթը համընկնի կոորդինատների սկզբնակետի՝

O (0; 0)

կետի հետ, իսկ էջերը գտնվեն կոորդինատային առանցքների վրա:

Եթե եռանկյան էջերը հավասար են՝

AO = b, BO = a

, ապա եռանկյան գագաթներն ունեն հետևյալ կոորդինատները՝

A (0; b), O (0; 0), B (a; 0)

(տես ներքևի նկարը):

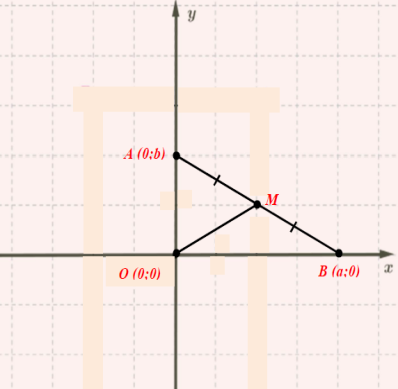
Ըստ հատվածների միջնակետի կոորդինատների հաշվման բանաձևի՝ գտնում ենք \(AB\) ներքնաձիգի \(M\) միջնակետի կոորդինատները՝

M (\frac{a}{2}; \frac{b}{2})

Օգտագործելով տրված ծայրակետերով հատվածների երկարության բանաձևը՝ հաշվենք

MO, AM, BM

հատվածների երկարությունները և համոզվենք, որ դրանք հավասար են:

MO = \sqrt{{(\frac{a}{2})}^{2} + {(\frac{b}{2})}^{2}} = \frac{1}{2} \sqrt{a^{2} + b^{2}}

AM = \sqrt{{(\frac{a}{2})}^{2} + {(\frac{b}{2} - b)}^{2}} = \frac{1}{2} \sqrt{a^{2} + b^{2}}

BM = \sqrt{{(\frac{a}{2} - a)}^{2} + {(\frac{b}{2})}^{2}} = \frac{1}{2} \sqrt{a^{2} + b^{2}}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, Զանգակ, 2013

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ