Հատվածի միջնակետի կոորդինատները

Դիտարկենք վերևի նկարի

O (0; 0)

C (2; 4)

կետերը միացնող

OC

հատվածը:

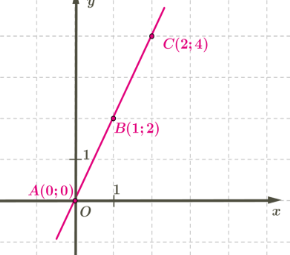
Նկարից երևում է, որ

OC

հատվածը \(2\) և \(4\) կողմերով ուղղանկյան անկյունագիծն է, և նրա միջնակետը

B (1; 2)

կետն է. ուղղանկյան անկյունագծերը հատվելիս կիսվում են:

Նկատում ենք, որ

B (1; 2)

կետի կոորդինատները

O (0; 0)

C (2; 4)

կետերի կոորդինատների միջոցով արտահայտվում են հետևյալ կերպ՝

1 = \frac{0 + 2}{2}, 2 = \frac{0 + 4}{2}

Այս օրինաչափությունը տեղի ունի նաև ընդհանուր դեպքում:

Եթե կոորդինատային հարթության վրա վերցված են երկու կետեր՝

K (x_{0}; y_{0})

L (x_{1}; y_{1})

, ապա

KL

հատվածի

M (x; y)

միջնակետի կոորդինատները հավասար են՝

x = \frac{x_{0} + x_{1}}{2}, y = \frac{y_{0} + y_{1}}{2}

Այսպիսով, հարթության վրա տրված երկու կետերը միացնող հատվածի միջնակետի կոորդինատները հավասար են ծայրակետերի համապատասխան կոորդինատների միջին թվաբանականներին՝

x = \frac{x_{0} + x_{1}}{2}, y = \frac{y_{0} + y_{1}}{2}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի.Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, Զանգակ, 2013

Վերադառնալ թեմային

Հաջորդ տեսությունը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Հատվածի միջնակետի կոորդինատները

Տեսություն