

















Կոն
Գիտենք, որ կոնը կարելի է ստանալ՝ պտտելով ուղղանկյուն եռանկյունը իր էջերից որևէ մեկի շուրջ:
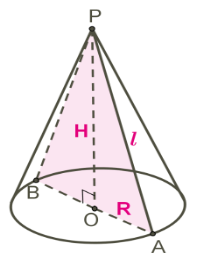
\(PO\) հատվածը կոչվում է կոնի բարձրություն:
Կոնի առանցքային հատույթը, որն անցնում է նրա գագաթով, հանդիսանում է \(PA\) և \(PB\) սրունքներով հավասարասրուն եռանկյուն: \(PA\)-ն և \(PB\)-ն կոչվում են կոնի ծնորդներ և նշանակվում են \(l\) տառով:
Եռանկյան պտույտից առաջացած \(O\) կենտրոնով շրջանը կոչվում է կոնի հիմք:
Կոնի շառավիղ կոչվում է նրա հիմքի \(R\)\(=\)\(OA\)\(=\)\(OB\) շառավիղը: 
Կոնի կողմնային մակերևույթի բացվածքը շրջանային սեկտոր է:

Այդ սեկտորի շառավիղը հավասար է կոնի ծնորդին՝ \(l\)-ի, իսկ աղեղի երկարությունը հավասար է կոնի հիմքի շրջանագծի երկարությանը՝
Ինչպես գիտենք, շրջանային սեկտորի մակերեսը հավասար է նրա շառավղի և աղեղի երկարության արտադրյալի կեսին:
Ստանում ենք՝
Այսպիսով, կոնի կողմնային մակերևույթի (կոնային մակերևույթի) մակերեսը հաշվում են բանաձևով:
Լրիվ մակերևույթի մակերեսը ստանալու համար պետք է գումարել հիմքի շրջանի մակերեսը՝
Փակագծերից դուրս բերելով ընդհանուր արտադրիչները, ստանում ենք՝
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ» 2013