Շրջանի մակերեսը — դաս։ Երկրաչափություն, 9-րդ դասարան.

Շրջանի մակերեսը

Դիտարկենք \(O\) կենտրոնով \(R\) շառավղով \(A\) շրջանագիծը, որը արտագծված է \(Q\) կանոնավոր բազմանկյանը: \(P\) բազմանկյանը, իր հերթին ներգծված է նույն \(O\) կենտրոնով և \(r\) շառավղով \(B\) շրջանագիծը:

\(A\) շրջանագծով սահմանափակված շրջանի մակերեսը նշանակենք \(S\)-ով և հաշվենք այն:

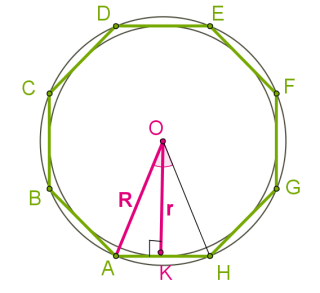
Հասկանալի է, որ այս երեք պատկերների մակերեսների համար տեղի ունի

S_{B} < S_{Q} < S

անհավասարությունը:

Գիտենք, որ \(Q\) բազմանկյան մակերեսը հավասար է՝

S_{Q} = \frac{P \cdot r}{2}

, որտեղ \(P\)-ն բազմանկյան պարագիծն է:

Տեղադրենք \(Q\) բազմանկյան մակերեսի արժեքը անհավասարության մեջ և անհավասարության երեք մասերը բաժանենք \(R\) շառավղի վրա: Ստանում ենք հետևյալ անհավասարությունը՝

\frac{S_{B}}{R} < \frac{P}{2} \cdot \frac{r}{R} < \frac{S}{R}

Պատկերացնենք, որ \(Q\) բազմանկյան գագաթների \(n\) թիվը անվերջ մեծանում է:

Այդ դեպքում ներգծյալ շրջանագիծը անվերջ մոտենում է արտագծյալ շրջանագծին, և հետևաբար, նրա շառավիղն ու նրանով սահմանափակված շրջանի մակերեսը անվերջ մոտենում են արտագծյալ շրջանագծի շառավղին և նրանով սահմանափակված շրջանի մակերեսին՝

r \to R, S_{B} \to S, երբ n \to \infty

\(Q\) բազմանկյան \(P\) պարագիծը, իր հերթին, անվերջ մոտենում է \(A\) շրջանագծի երկարությանը՝

P \to 2 π R

Այսպիսով, \(n\) թիվը անվերջ մեծանալիս անհավասարությունը ընդունում է այս տեսքը՝

\begin{array}{l} \frac{S}{R} \leq \frac{2 π R}{2} \cdot \frac{R}{R} \leq \frac{S}{R} \\ \frac{S}{R} = π R \\ S = π R^{2} \end{array}

Շրջանի մակերեսը հաշվում են

S = π \cdot R^{2}

բանաձևով:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ» 2013

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Շրջանի մակերեսը

Տեսություն