Սեգմենտի մակերեսը — դաս։ Երկրաչափություն, 9-րդ դասարան.

Սեգմենտի մակերեսը

Սեգմենտ կոչվում է շրջանի այն մասը, որը սահմանափակված է աղեղով և այդ աղեղի ծայրակետերը միացնող լարով:

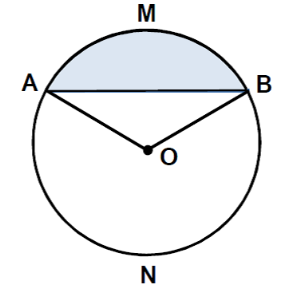
Դիտարկենք վերևի նկարի վրա ցուցադրված սեգմենտը (կապույտով նշված), որը սահմանափակված է \(AMB\) աղեղով և \(AB\) լարով:

Նկարից երևում է, որ այդ սեգմենտի մակերեսը հավասար է՝

S_{սեգմենտ} = S_{սեկտոր} - S_{Δ AOB}

Նկարում պատկերված շրջանագծի վրա \(A\) և \(B\) ծայրակետերով կա ևս մեկ աղեղ՝ \(ANB\)

Այդ աղեղով և \(AB\) լարով ևս սահմանափակվում է սեգմենտ:

Այդ սեգմենտի մակերեսը հավասար է՝

S_{սեգմենտ} = S_{սեկտոր} + S_{Δ AOB}

Նկատենք, որ առաջին սեգմենտի \(AMB\) աղեղի աստիճանային չափը փոքր է

180 °

-ից, իսկ երկրորդ սեգմենտի \(ANB\) աղեղի աստիճանային չափը մեծ է

180 °

-ից:

Հիշենք

α

աստիճանային չափով սեկտորի մակերեսի հաշվման բանաձևը՝

S_{սեկտոր} = \frac{π R^{2}}{360 °} \cdot α

Տեղադրելով սեկտորի մակերեսի արժեքը դիտարկված երկու սեգմենտների բանաձևերի մեջ, գալիս ենք հետևյալ եզրակացությանը:

1) Եթե

α

\(<\)

180 °

, ապա

S_{սեգմենտ} = \frac{π R^{2}}{360 °} \cdot α - S_{Δ}

2) Եթե

α

\(>\)

180 °

, ապա

S_{սեգմենտ} = \frac{π R^{2}}{360 °} \cdot α + S_{Δ}

Եթե

α

\(=\)

180 °

, ապա \(AB\) լարը դառնում է տրամագիծ: Այս դեպքում երկու սեգմենտները կազմում են շրջանի երկու կիսաշրջանները, և նրանց մակերեսները հավասար են՝

\frac{π \cdot R^{2}}{2}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ» 2013

Սխա՞լ ես գտել

1. Սեգմենտի մակերեսը