Կանոնավոր բազմանկյուններ — դաս։ Երկրաչափություն, 9-րդ դասարան.

Կանոնավոր բազմանկյուններ

Կանոնավոր կոչվում են այն բազմանկյունները, որի բոլոր կողմերն ու բոլոր անկյունները հավասար են:

Ներքևի նկարում բերված են կանոնավոր բազմանկյունների օրինակներ՝ հավասարակողմ եռանկյուն, քառակուսի, կանոնավոր հնգանկյուն և վեցանկյուն:

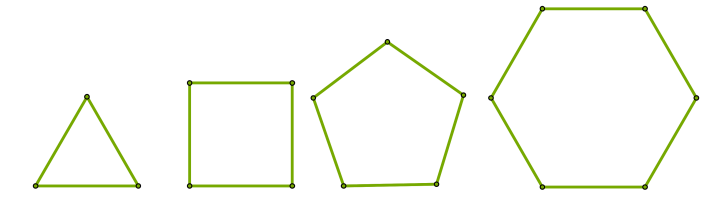
Եթե կամայական կանոնավոր \(n\)-անկյան միևնույն գագաթից տանել անկյունագծեր, ապա բազմանկյունը կբաժանվի \(n-2\) եռանկյունների: Ուստի, կանոնավոր բազմանկյան ներքին անկյունների գումարը հավասար է

180 ° \cdot (n - 2)

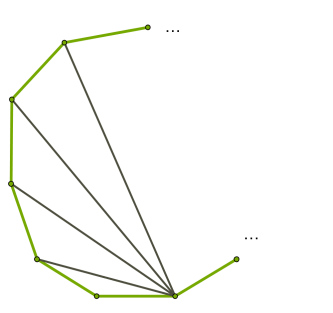
Քանի որ կանոնավոր \(n\)-անկյան բոլոր ներքին անկյունները հավասար են, ապա մեկ անկյան մեծությունը կլինի՝

\frac{180 ° \cdot (n - 2)}{n}

Ցանկացած կանոնավոր բազմանկյանը կարելի է ներգծել և արտագծել շրջանագծեր: Ընդ որում, այդ շրջանագծերի կենտրոնները համընկնում են:

Ներգծյալ շրջանագիծը շոշափում է բազմանկյան բոլոր կողմերը, իսկ արտագծյալ շրջանագիծը անցնում է բոլոր գագաթներով:

∡ AOH = \frac{360 °}{n}; ∡ AOK = \frac{360 °}{2n} = \frac{180 °}{n}

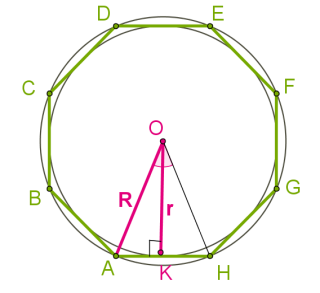
\(AOK\) եռանկյան մեջ գոյություն ունեն կապեր \(a\) կողմի (\(AK\) հատվածը), արտագծյալ շրջանագծի շառավիղի՝ \(OA = R\) և ներգծյալ շրջանագծի շառավղի՝ \(OK = r\) միջև:

\begin{array}{l} \frac{a}{2} = R \cdot \sin \frac{180 °}{n}; a = 2 R \cdot \sin \frac{180 °}{n}; R = \frac{a}{2 \sin \frac{180 °}{n}} \\ \frac{a}{2} = r \cdot tg \frac{180 °}{n}; a = 2 r \cdot tg \frac{180 °}{n}; r = \frac{a}{2 tg \frac{180 °}{n}} \\ r = R \cdot \cos \frac{180 °}{n}; R = \frac{r}{\cos \frac{180 °}{n}} \end{array}

Քանի որ \(n\)-անկյունը բաղկացած է \(n\) հատ եռանկյուններից, որոնցից յուրաքանչյուրը հավասար է \(AOH\) եռանկյանը, ապա՝

S_{n} = n \cdot S_{AOK} = n \cdot \frac{AH \cdot r}{2} = \frac{p \cdot r}{2}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ», 2013

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Կանոնավոր բազմանկյուններ

Տեսություն