Վեկտորների սկալյար արտադրյալ

Երկու վեկտորների սկալյար արտադրյալ կոչվում է նրանց երկարությունների և իրենցով կազմված անկյան կոսինուսի արտադրյալը:

\vec{a}

\vec{b}

վեկտորների սկալյար արտադրյալը թիվ է, որը հավասար է ՝

\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos α

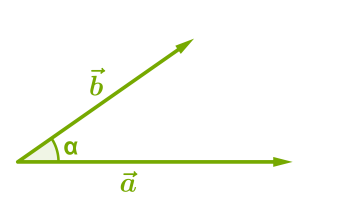
Կարևոր է ճիշտ որոշել վեկտորների կազմած անկյունը: Եթե վեկտորների սկզբնակետերը չեն համընկում, ապա պետք դրանք տեղադրել նույն կետից:

Վեկտորների կազմած անկյունը նշանակում են այսպես՝

\hat{\vec{a} \vec{b}} = α

1. Եթե վեկտորները համուղղված են, ապա՝

\hat{\vec{a} \vec{b}} = 0 °

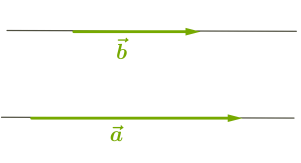
Ուշադրություն

Քանի որ \(0\) աստիճանի անկյան կոսինուսը հավասար է \(1\)-ի, ապա համուղղված վեկտորների սկալյար արտադրյալը հավասար է նրանց երկարությունների արտադրյալին:

2. Եթե վեկտորները հակուղղված են, ապա

\hat{\vec{a} \vec{b}} = 180 °

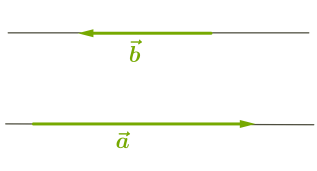
Ուշադրություն

Քանի որ \(180\) աստիճանի անկյան կոսինուսը հավասար է \(-1\)-ի, ապա հակուղղված վեկտորների սկալյար արտադրյալը հավասար է դրանց երկարությունների արտադրյալին, վերցված մինուս նշանով:

3. Եթե վեկտորները ուղղահայաց են, ապա

\hat{\vec{a} \vec{b}} = 90 °

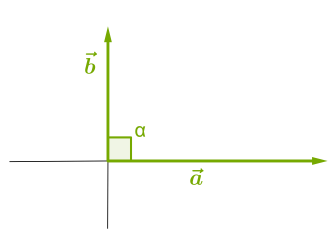
Ուշադրություն

Քանի որ ուղիղ անկյան կոսինուսը հավասար է \(0\)-ի, ապա ուղղահայաց վեկտորների սկալյար արտադրյալը հավասար է \(0\)-ի:

Ճիշտ է նաև հակառակ պնդումը՝ եթե վեկտորների սկալյար արտադրյալը հավասար է զրոյի, ապա դրանք ուղղահայաց են:

Այսպիսով՝ երկու վեկտորների սկալյար արտադրյալը հավասար է \(0\)-ի այն և միայն այն դեպքում, երբ դրանք ուղղահայաց են:

4. Դիտարկենք բութ անկյուն կազմող վեկտորների սկալյար արտադրյալը:

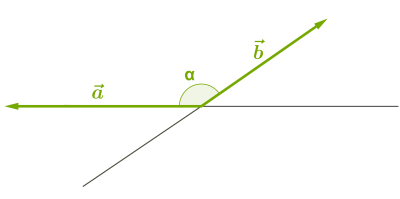
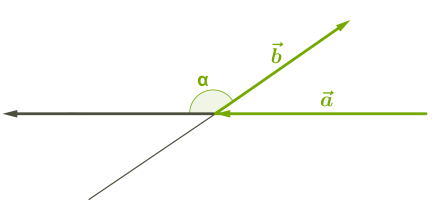
Ուշադրություն

Քանի որ բութ անկյան կոսինուսը բացասական է, ապա վեկտորների սկալյար արտադրյալը բացասական թիվ է:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, Զանգակ, 2013

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Վեկտորների սկալյար արտադրյալ

Տեսություն