Եռանկյան լուծումը — դաս։ Երկրաչափություն, 9-րդ դասարան.

Եռանկյան լուծումը

Եռանկյան լուծում անվանում են նրա վեց տարրերի (երեք կողմեր, երեք անկյուններ) գտնելը, եռանկյունը որոշող որևէ երեք տարրերի միջոցով:

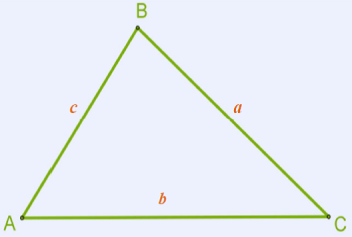
Խնդիր 1. Տրված են \(a\), \(b\) կողմերը և \(C\) անկյունը:

Պետք է գտնել \(c\) կողմը և \(A\), \(B\) անկյունները:

Լուծում: 1. Ըստ կոսինուսների թեորեմի գտնում ենք \(c\) կողմը՝

c = \sqrt{a^{2} + b^{2} - 2 \cdot a \cdot b \cdot \cos C}

2. Ունենալով եռանկյան բոլոր երեք կողմերը, կոսինուսների թեորեմի միջոցով գտնում ենք \(A\) անկյան կոսինուսը՝

\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 bc}

Անկյունը գտնում ենք հաշվիչի կամ եռանկյունաչափական աղյուսակների միջոցով:

3. Նույն ձևով կարելի է գտնել \(B\) անկյունը, սակայն ավելի հեշտ է \(B\) անկյունը գտնել \(A\) և \(C\) անկյունների միջոցով՝

∠ B = 180 ° - ∠ A - ∠ C

Խնդիր 2. Տրված է \(a\) կողմը և \(B\), \(C\) անկյունները:

Պետք է գտնել \(A\) անկյունը և \(b\), \(c\) կողմերը:

Լուծում: 1. \(B\), \(C\) անկյունների միջոցով գտնում ենք \(A\) անկյունը՝

∠ A = 180 ° - ∠ B - ∠ C

2. Սինուսների թեորեմի միջոցով գտնում ենք \(b\) և \(c\) կողմերը՝

b = a \frac{\sin B}{\sin A}, c = a \frac{\sin C}{\sin A}

Խնդիր 3. Տրված են \(a\), \(b\), \(c\) կողմերը:

Պետք է գտնել \(A\), \(B\), \(C\) անկյունները:

Լուծում: 1. Ըստ կոսինուսների թեորեմի ստանում ենք \(A\) անկյան կոսինուսը՝

\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 bc}

Անկյունը գտնում ենք հաշվիչի կամ եռանկյունաչափական աղյուսակների միջոցով:

2. Նույն ձևով հաշվում ենք \(B\) և \(C\) անկյունները:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ», 2013

Սխա՞լ ես գտել

1. Եռանկյան լուծումը