Անկյան սինուսը, կոսինուսը և տանգենսը

Կոորդինատային հարթության մեջ կառուցենք \(1\) շառավղով կիսաշրջանագիծ, որի կենտրոնը կոորդինատների սկզբնակետն է: Այն անվանենք միավոր կիսաշրջանագիծ:

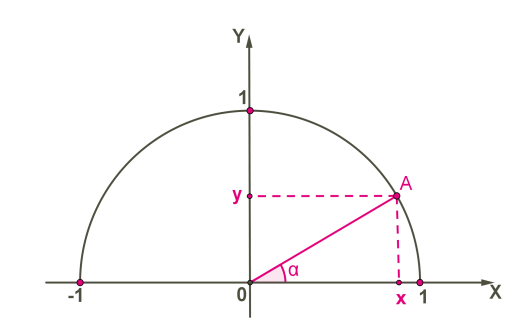
Դիտարկենք

α

սուր անկյունով \(AOX\) ուղղանկյուն եռանկյունը:

Գիտենք, որ սուր անկյան սինուսը հավասար է անկյան դիմացի էջի հարաբերությանը ներքնաձիգին, իսկ կոսինուսը՝ կից էջի հարաբերությանը ներքնաձիգին:

Այսպիսով՝

\sin α = \frac{AX}{AO}; \cos α = \frac{OX}{AO}

քանի որ կիսաշրջանագծի շառավիղը \(R = AO = 1\), ապա

\sin α = AX; \cos α = OX

0 ° \leq α \leq 180 °

միջակայքի ցանկացած

α

անկյան սինուս կոչվում է \(A\) կետի \(y\) կոորդինատը, իսկ կոսինուս՝ այդ կետի \(x\) կոորդինատը՝

A (\cos α; \sin α)

Հետևաբար,

0 ° \leq α \leq 180 °

միջակայքի ցանկացած անկյան համար տեղի ունեն հետևյալ անհավասարությունները՝

- 1 \leq \cos α \leq 1; 0 \leq \sin α \leq 1

α

անկյան

(α \neq 90 °)

տանգենս կոչվում է

tg α = \frac{\sin α}{\cos α}

հարաբերությունը:

α

անկյան

(α \neq 0 °, 180 °)

կոտանգենս կոչվում է

ctg α = \frac{\cos α}{\sin α}

հարաբերությունը:

Տանգենսի

(α \neq 90 °)

և կոտանգենսի

(α \neq 0 °, 180 °)

արժեքները որոշված չեն նշված անկյունների դեպքում, քանի որ դրանց համար կոտորակների հայտարարները հավասար են զրոյի:

Քանի որ

ctg α = \frac{1}{tg α}

, ապա կոտանգենսի կիրառությունը փոխարինվում են տանգենսով:

Բերված սահմանումների միջոցով և օգտագործելով միավոր շրջանագիծը, ստանում ենք

0 °; 90 °; 180 °

անկյունների սինուսի, կոսինուսի և տանգենսի արժեքները՝

\begin{array}{l} \sin 0 ° = 0; \cos 0 ° = 1; tg 0 ° = 0 \\ \sin 90 ° = 1; \cos 90 ° = 0; tg 90 ° գոյություն չունի \\ \sin 180 ° = 0; \cos 180 ° = - 1; tg 180 ° = 0 \end{array}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, "Զանգակ", 2013

Սխա՞լ ես գտել

1. Անկյան սինուսը, կոսինուսը և տանգենսը