
















Շրջանագծի շոշափող
Եթե շրջանագծի կենտրոնի հեռավորությունն ուղղից հավասար է շրջանագծի շառավղին, ապա շրջանագիծն ու ուղիղը ունեն մեկ ընդհանուր կետ:
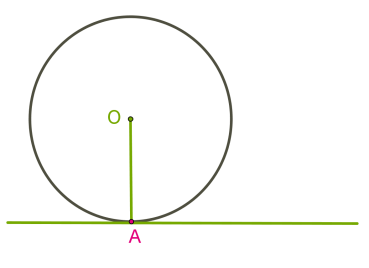
Այդ դեպքում ուղիղն անվանում են շրջանագծի շոշափող:
Եթե ուղիղը շրջանագծի հետ ունի մեկ ընդհանուր կետ, ապա այն կոչվում է շրջանագծի շոշափող:
Շրջանագծի շոշափողը ուղղահայաց է շոշափման կետից տարված շառավղին:
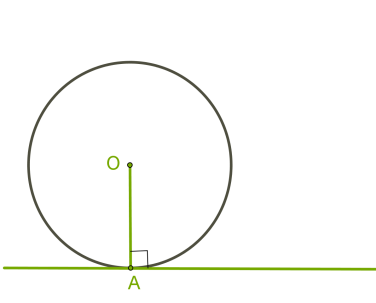
Ենթադրենք, թե \(OA\) շառավիղն ուղղահայաց չէ շոշափողին, այլ թեք է: Ապա, \(O\) կետից կարելի է տանել ուղղին ուղղահայաց, որը կլինի շառավղից փոքր: Սա նշանակում է, որ շրջանագծի կենտրոնի հեռավորությունն ուղղից ավելի փոքր է, քան շառավիղը, ուրեմն, շրջանագիծն ու ուղիղը պիտի ունենան երկու ընդհանուր կետեր: Սա հակասում է այն փաստին, որ ուղիղը շոշափող է: Հետևաբար, մեր ենթադրությունը սխալ էր:
Եթե միևնույն կետից շրջանագծին տարված են երկու շոշափողներ, ապա
ա) շոշափման կետերի հեռավորությունները տրված կետից հավասար են,
բ) շրջանագծի կենտրոնով և տրված կետով անցնող ուղիղը կիսում է շոշափողների կազմած անկյունը:
Օրինակ
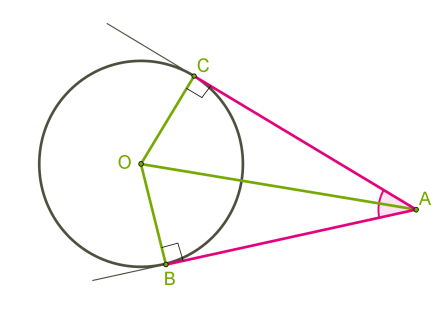
Դիցուք \(AB\) -ն և \(AC\) -ն \(O\) կենտրոնով շրջանագծի շոշափողներն են: Պետք է ապացուցել, որ \(AB = AC\) և \(OA\) -ն \(A\) անկյան կիսորդն է:
\(OBA\) և \(OCA\) եռանկյուններն ուղղանկյուն են, քանի որ շոշափողները ուղղահայաց են շառավիղներին \(B\) և \(C\) կետերում: \(OA\) կողմն ընդհանուր է: \(OB\) և \(OC\) էջերը հավասար են, որպես նույն շրջանագծի շառավիղներ: Ուղղանկյուն եռանկյունները հավասար են, ըստ՝ ներքնաձիգի և էջի: Հետևաբար, հավասար են նաև մյուս էջերը՝ \(AB\) -ն և \(AC\) -ն, և \(BAO\) և \(CAO\) անկյունները: \(A\) անկյունը կիսվեց:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007: