1. Պտտման մարմիններ

Գլան կարելի է ստանալ՝ պտտելով $A{A}_1{O}_{1}O$ ուղղանկյունը իր կողմերից որևէ մեկի, օրինակ՝ $O{O}_1$-ի շուրջ: Նույն գլանը կարելի է ստանալ՝ պտտելով $A{A}_1{B}_{1}B$ ուղղանկյունն իր հանդիպակաց կողմերի միջնակետերով անցնող $O{O}_1$ ուղղի շուրջ:

 

 

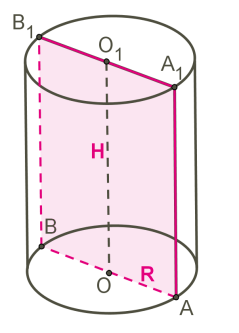
$O{O}_1$ ուղիղը կոչվում է գլանի առանցք, $A{A}_1$-ը և $B{B}_1$-ը՝ ծնորդներ: Գլանի \(H\) բարձրությունը հավասար է $O{O}_1$\(=\)$A{A}_1$\(=\)$B{B}_1$ հատվածներից յուրաքանչյուրին:

 

Պտտման ընթացքում առաջացած երկու շրջանները կոչվում են գլանի հիմքեր:

 

Գլանի \(R\)\(=\)\(OA\)\(=\)\(OB\) շառավիղ կոչվում է նրա հիմքի շառավիղը:

Գլանի առանցքով անցնող հարթության և գլանի ընդհանուր մասը կոչվում է գլանի առանցքային հատույթ: Գլանի առանցքային հատույթը ուղղանկյուն է: Վերևի նկարում դա $A{A}_1{B}_{1}B$ ուղղանկյունն է:

Գլանի կողմնային մակերևույթի բացվածքը ևս ուղղանկյուն է:

 

Այդ ուղղանկյան կողմերից մեկը հիմքի շրջանագծի երկարությունն է, իսկ մյուսը՝ գլանի բարձրությունը: Ուրեմն, գլանի կողմնային մակերևույթի մակերեսը հավասար է՝

 

Եթե սրան գումարենք երկու հիմքերի մակերեսները, ապա կստանանք գլանի լրիվ մակերևույթի մակերեսը՝

 

Կոնը կարելի է ստանալ՝ պտտելով \(POA\) ուղղանկյուն եռանկյունը իր էջերից որևէ մեկի, օրինակ՝ \(PO\)-ի շուրջ: Նույն կոնը կստացվի, եթե \(APB\) հավասարասրուն եռանկյունը պտտենք \(PO\) բարձրության շուրջ:

 

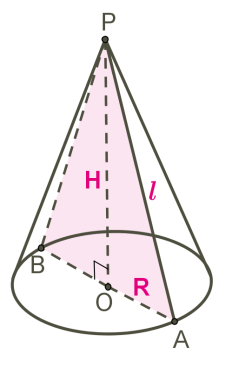
\(PO\) ուղիղը կոչվում է կոնի առանցք, որը պարունակում է կոնի \(H\) բարձրությունը:

Կոնի առանցքային հատույթը, որը անցնում է նրա գագաթով, հանդիսանում է \(PA\) և \(PB\) սրունքներով հավասարասրուն եռանկյուն: \(PA\)-ն և \(PB\)-ն կոչվում են կոնի ծնորդներ և նշանակվում են \(l\) տառով:

 

Եռանկյան պտույտից առաջացած \(O\) կենտրոնով շրջանը կոչվում է կոնի հիմք:

 

Կոնի շառավիղ կոչվում է նրա հիմքի \(R\)\(=\)\(OA\)\(=\)\(OB\) շառավիղը:

 

 

Սեկտորի շառավիղը հավասար է \(l\)-ի:

 

 

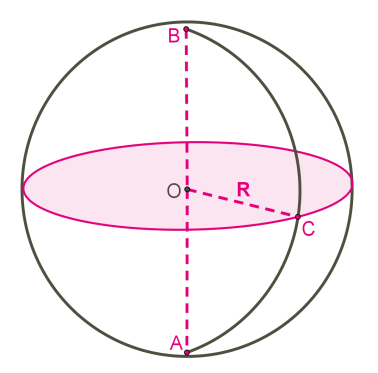
Գնդի մակերևույթը (գնդային մակերևույթը) կոչվում է գնդոլորտ (սֆերա): Գնդոլորտը ստացվում է կիսաշրջանագծի կամ շրջանագծի պտույտի միջոցով:

 

Գնդոլորտին են պատկանում գնդի բոլոր այն կետերը, որոնց հեռավորությունը գնդի \(O\) կենտրոնից հավասար է \(R\) շառավղին:

  

\(OA\)-ն, \(OB\)-ն և \(OC\)-ն, կամ ցանկացած այլ հատված, որը միացնում է գնդոլորտի կետը գնդի կենտրոնի հետ, կոչվում է գնդի շառավիղ:

  

 Գնդի երկու կետեր միացնող հատվածը, որը անցնում է գնդի կենտրոնով, կոչվում է գնդի տրամագիծ: Վերևի նկարում դա \(AB\) հատվածն է:

Կենտրոնով անցնող գնդի հատույթը կոչվում է մեծ շրջան, իսկ գնդոլորտի հատույթը՝ մեծ շրջանագիծ:

Գնդոլորտի մակերեսը հաշվում են հետևյալ բանաձևով՝