
















Կենտրոնային և ներգծյալ անկյուններ
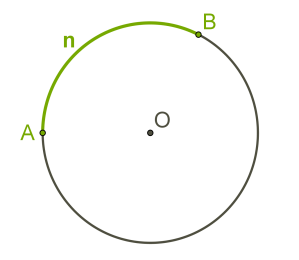
Այդ երկու աղեղներն իրարից տարբերելու համար օգտագործում են նշանակման մի քանի ձև: Ձևերից մեկում օգտագործում են լատիներեն փոքրատառեր՝ : Նաև կարելի է շրջանագծի վրա վերցնել երրորդ միջանկյալ \(C\) կետը: Այն կպատկանի աղեղներից մեկին և չի պատկանի մյուսին: Այս դեպքում \(ACB\) -ն նշանակում է այն աղեղը, որին պատկանում է \(C\) կետը:
Ցանկացած աղեղ ունի աստիճանային չափ: Մեր դիտարկած երկու աղեղների աստիճանային չափերի գումարը տալիս է լրիվ անկյան չափը՝ : Եթե վերցված կետերը միացնող հատվածը տրամագիծ է, ապա աղեղն անվանում են կիսաշրջանագիծ: Կիսաշրջանագծի աստիճանային չափը է:
Կենտրոնային և ներգծյալ անկյուններ
Այն անկյունը, որի գագաթը շրջանագծի կենտրոնն է, կոչվում է կենտրոնային անկյուն:
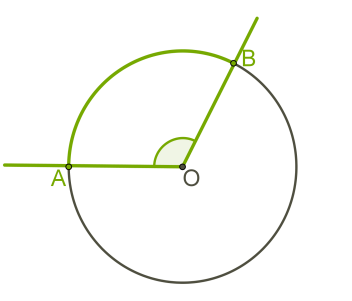
Աղեղի աստիճանային չափը հավասար է համապատասխան կենտրոնային անկյան աստիճանային չափին՝ \(AOB =\)\(AB\)
Այն անկյունը, որի գագաթն ընկած է շրջանագծի վրա, իսկ կողմերը շրջանագիծը հատում են, կոչվում է ներգծյալ անկյուն:
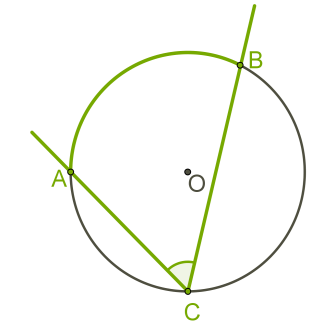
Ներգծյալ անկյունը չափվում է այն աղեղի կեսով, որի վրա նա հենվում է՝
1. Նույն աղեղի վրա հենված ներգծյալ անկյունները հավասար են:
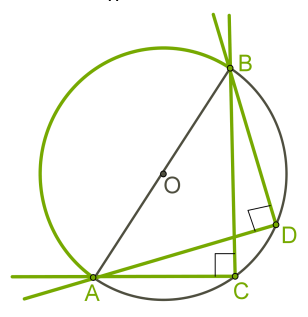
2. Կիսաշրջանագծի վրա հենված ներգծյալ անկյունը է:
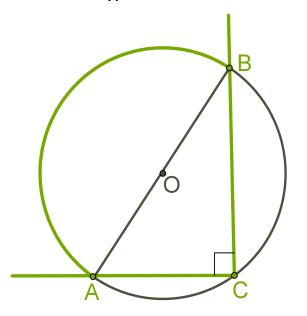
Շրջանագծի հատվող լարերի հատկությունը
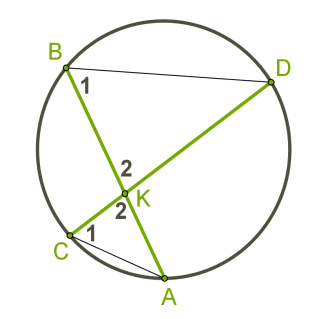
Եթե շրջանագծի երկու լարեր հատվում են, ապա մի լարի հատվածների արտադրյալը հավասար է մյուս լարի հատվածների արտադրյալին:
Այս հատկությունն ապացուցվում է եռանկյունների նմանության գաղափարի օգնությամբ՝ : Այս գաղափարը կուսումնասիրենք հետագայում:
Նշենք, որ ապացույցի հիմքում ընկած է այն փաստը, որ նշված եռանկյունների բոլոր երեք անկյունները համապատասխանաբար հավասար են՝ անկյունները նույն աղեղի վրա հենված ներգծյալ անկյուններ են, իսկ անկյունները՝ հակադիր են:
Այսպիսով՝
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007: