
















Երկու շրջանագծերի փոխադարձ դասավորությունը
Հարթության մեջ երկու շրջանագծերի փոխադարձ դասավորությունը կախված է՝
- նրանց կենտրոնների դասավորությունից,
- նրանց շառավիղների երկարություններից:
Հնարավոր է երեք դեպք:
1) Երկու շրջանագծերը հատվում են՝ ունեն երկու ընդհանուր կետ:
2) Երկու շրջանագծերը շոշափում են՝ ունեն մեկ ընդհանուր կետ:
3) Երկու շրջանագծերը ընդհանուր կետեր չունեն:
Դիտարկենք հնարավոր դեպքերը:
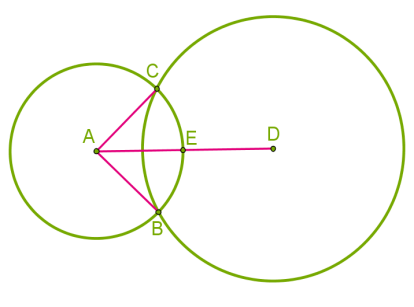
1) Երկու շրջանագծերը հատվում են. ունեն երկու ընդհանուր կետ:
Այս դեպքում կենտրոնների հեռավորությունը փոքր է շառավիղների գումարից:
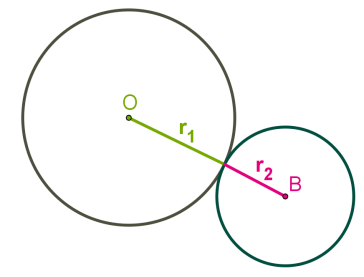
2) Երկու շրջանագծերը շոշափում են. ունեն մեկ ընդհանուր կետ:
Այս դեպքում հնարավոր են հետևյալ դեպքերը՝
- արտաքին շոշափում,
- ներքին շոշափում:
Արտաքին շոշափման ժամանակ կենտրոնների հեռավորությունը հավասար է շառավիղների գումարին:
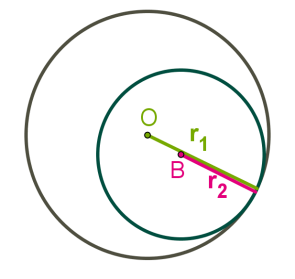
Ներքին շոշափման ժամանակ կենտրոնների հեռավորությունը հավասար է շառավիղների տարբերությանը:
3) Երկու շրջանագծերը ընդհանուր կետեր չունեն:
Այս դեպքում ևս հնարավոր է երկու դեպք:
- Երկու շրջանագծերով սահմանափակված շրջանները չեն հատվում:
- Փոքր շառավղով շրջանը ընկած է մեծ շառավղով շրջանի մեջ:
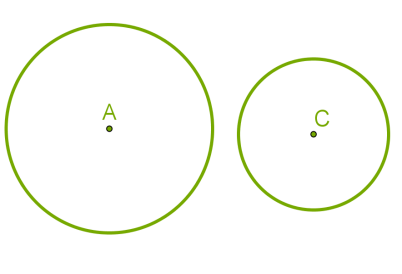
Առաջին տարբերակում կենտրոնների հեռավորությունը մեծ է շառավիղների գումարից:

Երկրորդ տարբերակում կենտրոնների հեռավորությունը փոքր է շառավիղների տարբերությունից:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007: