
















Թալեսի* թեորեմը
Եթե անկյան կողմերը հատող զուգահեռ ուղիղները անկյան մի կողմի վրա անջատում են հավասար հատվածներ, ապա նրանք անկյան մյուս կողմի վրա ևս անջատում են հավասար հատվածներ:
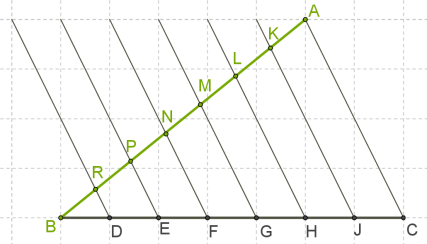
Պետք է \(AB\) հատվածը բաժանել 7 հավասար մասերի:
Գծենք անկյուն, որի մի կողմի վրա ընկած է \(AB\) հատվածը: \(BC\) կողմը գծենք վանդակների միջոցով՝ հորիզոնական ուղղությամբ: Վանդակները օգտագործում ենք կողմը 7 հավասար մասերի բաժանելու համար՝ \(BD = DE = EF = FG = GH = HJ = JC\):
Երկու հատվածների ծայրակետերը միացնում ենք և ստանում \(AC\) հատվածը: \(J, H, G, F, E, D\) կետերից տանենք \(AC\) -ին զուգահեռ \(7\) ուղիղներ (նորից օգտագործում ենք վանդակները):
Գծենք անկյուն, որի մի կողմի վրա ընկած է \(AB\) հատվածը: \(BC\) կողմը գծենք վանդակների միջոցով՝ հորիզոնական ուղղությամբ: Վանդակները օգտագործում ենք կողմը 7 հավասար մասերի բաժանելու համար՝ \(BD = DE = EF = FG = GH = HJ = JC\):
Երկու հատվածների ծայրակետերը միացնում ենք և ստանում \(AC\) հատվածը: \(J, H, G, F, E, D\) կետերից տանենք \(AC\) -ին զուգահեռ \(7\) ուղիղներ (նորից օգտագործում ենք վանդակները):
Եթե \(BD = DE = EF = FG = GH = HJ = JC\) և \(AC\)\(JK\)\(HL\)\(GM\)\(FN\)\(EP\)\(DR\), ապա, ըստ Թալեսի թեորեմի՝ \(BR = RP = PN = NM = ML = LK = KA\):
*Թեորեմը կոչվում է հին հույն գիտնական Թալես Միլեթացու (մ.թ.ա. մոտ 625-547 թթ.) անունով:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007: