
















Պրիզմա
Դիտարկենք հետևյալ բազմանիստը:
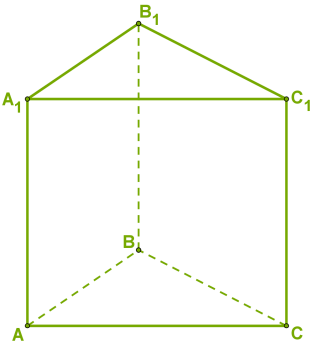
Այս բազմանիստի մակերևույթը կազմված է երկու հավասար եռանկյուններից (հիմքեր)՝ և , իսկ մյուս բոլոր նիստերը ուղղանկյուններ են:
Դիտարկենք ևս մեկ բազմանիստ:
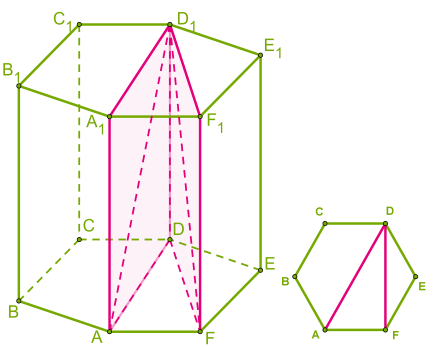
Այս բազմանիստի հիմքերը հավասար վեցանկյուններ են, իսկ մյուս բոլոր նիստերը ուղղանկյուններ են:
Բազմանիստների բերված երկու օրինակներում հիմքերը հավասար բազմանկյուններ են, իսկ մյուս բոլոր նիստերը ուղղանկյուններ են: Այդպիսի մարմինները կոչվում են ուղիղ պրիզմա:
Հավասար բազմանկյունները կոչվում են պրիզմայի հիմքեր:
Ուղղանկյունները կոչվում են կողմնային նիստեր:
Ուղիղ պրիզման կոչվում է կանոնավոր, եթե պրիզմայի հիմքերը կանոնավոր բազմանկյուններ են:
Բուրգ
Բուրգ կոչվում է այն բազմանիստը, որի մակերևույթը կազմված է որևէ բազմանկյունից (հիմք) և ընդհանուր գագաթ ունեցող եռանկյուններից, որոնց ընդհանուր գագաթի հանդիպակաց կողմերը հիմքի կողմերն են:
Բազմանկյունը կոչվում է բուրգի հիմք:
Եռանկյունները կոչվում են բուրգի կողմնային նիստեր:
Եռանկյունների ընդհանուր գագաթը կոչվում է բուրգի գագաթ:
Գագաթից դուրս եկող կողերը կոչվում են կողմնային կողեր:
Հիմքի բազմանկյան կողմերի թվից կախված ներքևի նկարի բուրգը կոչվում է վեցանկյուն բուրգ:
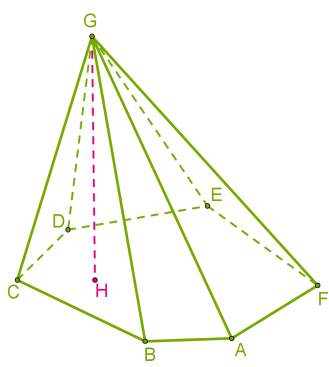
Հետևյալ բուրգը քառանկյուն բուրգ է:
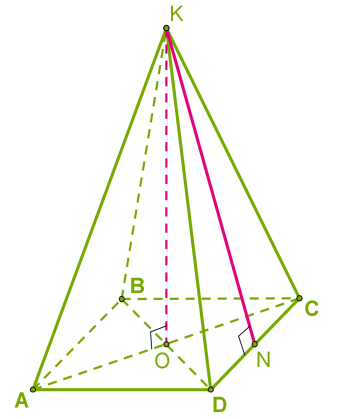
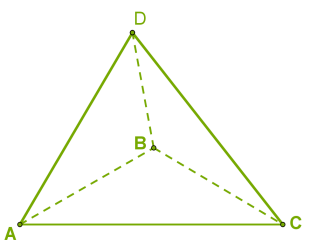
Իսկ այս մեկը՝ եռանկյուն բուրգ է:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007: