
















Զուգահեռագծի մակերեսը
Դա ուղղահայացն է, որը տարված է զուգահեռագծի կողմի ցանկացած կետից դեպի հանդիպակաց կողմը պարունակող ուղիղը:
\(BE\) բարձրությունը, որը տարված է երկու մեծ կողմերի միջև ավելի կարճ է, քան \(BF\)-ը, որը տարված է կարճ կողմերի միջև:
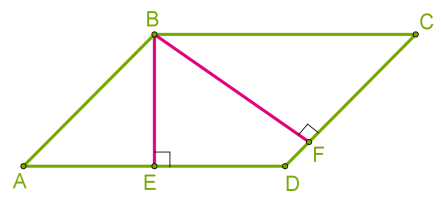
Զուգահեռագծի մակերեսը հավասար է նրա կողմի և նրան տարված բարձրության արտադրյալին:
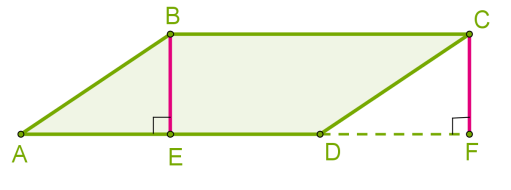
\(B\) և \(C\) գագաթներից տանենք բարձրություններ \(AD\) կողմին:
\(ABE\) և \(DCF\) ուղղանկյուն եռանկյունները հավասար են (հավասար ներքնաձիգներ՝ զուգահեռագծի հանդիպակաց կողմերը, և հավասար էջեր՝ հեռավորությունները զուգահեռ ուղիղների միջև):
\(ABCD\) զուգահեռագիծը և \(EBCF\) ուղղանկյունը հավասարամեծ են՝ ունեն հավասար մակերեսներ, քանի որ բաղկացած են հավասար պատկերներից:
Հետևաբար, զուգահեռագծի մակերեսը կարելի է հաշվել` հաշվելով ուղղանկյան մակերեսը՝
Եթե \(a\)-ով նշանակել կողմը, իսկ \(h\)-ով բարձրությունը, ապա՝
Շեղանկյան մակերեսը
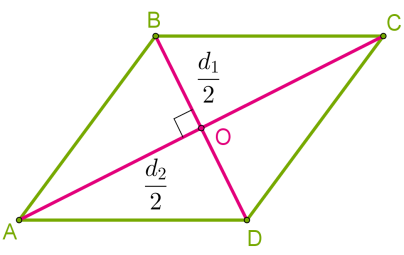
Շեղանկյան մակերեսի բանաձևը՝
Այս բանաձևը մնում է ուժի մեջ ցանկացած քառանկյան համար, որի անկյունագծերը փոխուղղահայաց են:
Քանի որ քառակուսու անկյունագծերը հավասար են, ապա նրա մակերեսը որոշելու համար բավական է ունենալ անկյունագծերից մեկի երկարությունը՝
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007: