Պյութագորասի թեորեմը — դաս։ Երկրաչափություն, 8-րդ դասարան.

Պյութագորասի թեորեմը

Պյութագորաս (մ.թ.ա. \(570 – 490\) թ.)՝ հույն մաթեմատիկոս և փիլիսոփա:

Պյութագորասի կենսագրության փաստերը հայտնի չեն: Նրա կյանքի մասին կարելի է դատել մյուս հույն փիլիսոփաների ստեղծագործությունների հիման վրա: Նրանց վկայությամբ Պյութագորասը շփվում էր իր ժամանակի ճանաչված մտածողների և գիտնականների հետ: Հայտնի է, որ Պյութագորասը երկար ժամանակ անցկացրել է Եգիպտոսում՝ ուսումնասիրելով տեղի ավանդույթներն ու հայտնագործությունները:

Մաթեմատիկայում Պյութագորասն ունեցավ մեծ հաջողություններ: Երկրաչափության ամենահայտնի թեորեմներից է Պյութագորասի թեորեմը, որի հայտնագործությունն ու ապացույցը վերագրվում է Պյութագորասին:

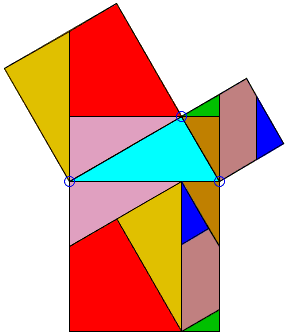
Ուղղանկյուն եռանկյան ներքնաձիգի վրա կառուցված քառակուսու մակերեսը հավասար է նրա էջերի վրա կառուցված քառակուսիների մակերեսների գումարին:

Մաթեմատիկայի պատմության մեջ գոյություն ունեն պնդումներ այն մասին, որ այդ թեորեմը գիտեին դեռևս Պյութագորասից շատ առաջ: Մասնավորապես, եգիպտացիները գիտեին, որ \(3\), \(4\) և \(5\) կողմերով եռանկյունը ուղղանկյուն եռանկյուն է:

Ներկայումս թեորեմը հնչում է այսպես՝

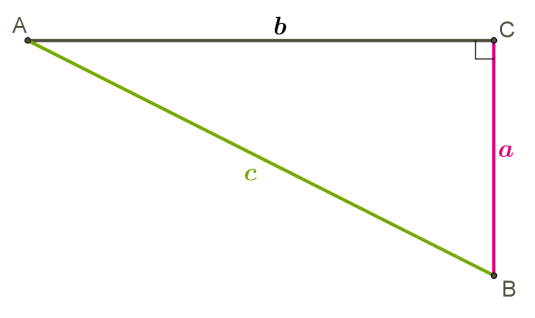
Ուղղանկյուն եռանկյան ներքնաձիգի քառակուսին հավասար է եռանկյան էջերի քառակուսիների գումարին՝

c^{2} = a^{2} + b^{2}

Հայտնի են այս թեորեմի բազմաթիվ ապացույցներ, սակայն ամենաակնառու ապացույցներից մեկը հիմնված է մակերեսների վրա:

1. Կառուցենք եռանկյան էջերի

a + b

գումարին հավասար կողմով քառակուսի: Քառակուսու մակերեսը

{(a + b)}^{2}

է:

2. Եթե տանենք \(c\) ներքնաձիգները, ապա կառուցված քառակուսու ներսում կառաջանա ևս քառանկյուն: Քառանկյան բոլոր կողմերը հավասար են \(c\)-ի, իսկ անկյունները՝ ուղիղ են: Իրոք, ուղղանկյուն եռանկյան սուր անկյունների գումարը

90 °

է, հետևաբար քառանկյան անկյունը ևս պիտի լինի

90 °

, որպեսզի նրանց գումարը հավասար լինի

180 °

-ի:

Այսպիսով, առաջացած քառանկյունը ևս քառակուսի է: Հետևաբար, մեծ քառակուսու մակերեսը բաղկացած է ներսի քառակուսու մակերեսից և չորս հավասար ուղղանկյուն եռանկյունների մակերեսներից:

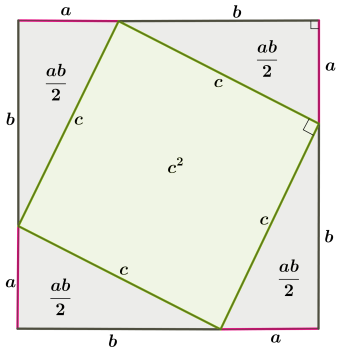
3. Մեծ քառակուսու երկու կողմերի վրա տեղերով փոխենք \(a\) և \(b\) հատվածները, դրանից քառակուսու կողմը չի փոխվի: Հիմա քառակուսու մակերեսը բաղկացած է (a\) և \(b\) կողմերով երկու քառակուսիներից և երկու ուղղանկյուններից՝

4. Համեմատելով մեծ քառակուսու մակերեսը երկու նկարներում, եզրակացնում ենք, որ՝

4 \cdot \frac{ab}{2} + c^{2} = a^{2} + 2 ab + b^{2}

, որտեղից գալիս ենք պահանջվող հավասարությանը՝

c^{2} = a^{2} + b^{2}

Ուշադրություն

Այս հավասարությունից կարելի է արտահայտել \(c\) ներքնաձիգը՝ \(a\) և \(b\) էջերի միջոցով՝

\begin{array}{l} c^{2} = a^{2} + b^{2} \\ c = \sqrt{a^{2} + b^{2}} \end{array}

Կարելի է նաև մի էջը արտահայտել ներքնաձիգի և մյուս էջի միջոցով՝

\begin{array}{l} a^{2} = c^{2} - b^{2} \\ a = \sqrt{c^{2} - b^{2}} \end{array}

Տեղի ունի նաև Պյութագորասի թեորեմի հակադարձ թեորեմը, որը կիրառվում է որպես ուղղանկյուն եռանկյան հայտանիշ:

Եթե եռանկյան մի կողմի քառակուսին հավասար է մյուս երկու կողմերի քառակուսիների գումարին, ապա այդ եռանկյունը ուղղանկյուն եռանկյուն է:

Օրինակ

Արդյո՞ք \(6\) սմ, \(7\) սմ և \(9\) սմ կողմերով եռանկյունը ուղղանկյուն եռանկյուն է:

Ընտրում ենք մեծ կողմը և ստուգում Պյութագորասի թեորեմի տեղի ունենալը՝

9^{2} = 6^{2} + 7^{2}; 81 \neq 36 + 49

Հետևաբար, եռանկյունը ուղղանկյուն չէ:

Արդյո՞ք \(5\) սմ, \(12\) սմ և \(13\) սմ կողմերով եռանկյունը ուղղանկյուն եռանկյուն է:

Ընտրում ենք մեծ կողմը և ստուգում Պյութագորասի թեորեմի տեղի ունենալը՝

13^{2} = 12^{2} + 5^{2}; 169 = 144 + 25

Հետևաբար, եռանկյունը ուղղանկյուն է:

Որպեսզի հաշվարկներ չկատարենք, օգտակար է հիշել Պյութագորասի առավել հաճախ պատահող թվերը՝

էջ, էջ, ներքնաձիգ

\(3; 4; 5\)

\(6; 8; 10\)

\(12; 16; 20\)

\(5; 12; 13\)

Դիտիր Պյութագորասի թեորեմի ևս մի յուրահատուկ ապացույց:

Աղբյուրները

http://linguaggio-macchina.blogspot.com

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Պյութագորասի թեորեմը

Տեսություն