
















Չափումներ
Չափումը չափման առարկայի համեմատումն է ընտրված չափման միավորի հետ:
Չափման մասին լավ պատկերացում է տալիս "\(38\) թութակ" մանկական մուլտֆիլմը: Այնտեղ լուծվում էր օձի երկարության չափման խնդիրը:

Թութակներով հաշված օձի երկարությունը հավասար էր 38 թութակի, կապիկներով հաշված՝ ստացվում էր 5 կապիկ, իսկ փղիկներով՝ \(2\) փղիկ: Բնականաբար, օձին դուր էր գալիս, որ թութակներով հաշված նա ավելի երկար էր: Այսպիսով, չափումների ժամանակ շատ կարևոր է չափման միավորի ընտրությունը:
Ուշադրություն
Եթե մենք ուզում ենք չափել մի քանի առարկաներ և համեմատել չափման արդյունքները, խիստ կարևոր է այդ առարկաները չափել միևնույն չափման միավորներով:
Առարկան չափելով՝ մենք իմանում ենք, թե քանի անգամ է առարկան մեծ (կամ փոքր) չափման միավորից: Կարող է պատահել, որ ընտրված չափման միավորը մեր առարկայի մեջ չի տեղավորվում՝ անգամ ամբողջ թվով: Այդ դեպքում չափման միավորը բաժանում են մասերի, իսկ մասերն էլ կարելի է շարունակել բաժանել ավելի փոքր մասերի՝ հնարավորինս ճշգրիտ չափում իրականացնելու համար: Իրավիճակից կախված, արդյունքը կարելի է կլորացնել և օգտագործել մոտավոր արժեքը:
Վերադառնալով օձի չափման մուլտֆիլմին՝ չափման ճշգրիտ արդյունքը հավասար էր 38 թութակ և մեկ թևիկ, սակայն ընդունվեց որոշում թևիկն անտեսել և արդյունքը կլորացնել մինչև ամբողջ միավորներ:
Հատվածի չափում
Հատվածի չափման համար որպես չափման գործիք ամենահաճախը օգտագործում են քանոն (լինում են շատ տարբեր քանոններ՝ ինչպես շատ մանր չափումների, այնպես էլ խոշորների համար):

Շատ հաճախ օգտագործվող չափման միավորներ են՝ \(1 կմ\), \(1 մ\), \(1 դմ\), \(1 սմ\), \(1 մմ\):
Հատվածի երկարության հատկությունները
\(1\). Հավասար հատվածներն ունեն հավասար երկարություններ:
\(2\). Հատվածի մի մասի երկարությունն ավելի փոքր է ամբողջ հատվածի երկարությունից:
\(3\). Եթե հատվածը կետերով բաժանվում է մասերի, ապա հատվածի գումարը հավասար է այդ մասերի երկարությունների գումարին:
Անկյան չափում
Անկախ չափման առարկայից, չափման մեծությունը ունի նույն հատկությունները:
Անկյան մեծության հատկությունները
\(1\). Հավասար անկյուններն ունեն հավասար մեծություններ:
\(2\). Անկյան մասի մեծությունը փոքր է ամբողջ անկյան մեծությունից:
\(3\). Եթե անկյան գագաթից դուրս եկող ճառագայթներով անկյունը բաժանվում է մասերի, ապա անկյան մեծությունը հավասար է այդ մասերի մեծությունների գումարին:
Անկյուն չափելու գործիքներից է անկյունաչափը:

Անկյան մեծության չափման միավոր է աստիճանը:

Սա այն աստիճանը չէ, որն օգտագործվում է ջերմաստիճան չափելու համար:
Անկյան չափման համար որպես չափման միավոր ընդունում են փռված անկյան մեծության -րդ մասը: Այսպիսով, փռված անկյան մեծությունը հավասար է \(180\) այդպիսի միավորի՝ աստիճանի:

Դա գրում են այսպես՝
Հետևաբար, քանի որ լրիվ անկյունը բաղկացած է երկու փռված անկյուններից, ապա նրա մեծությունը հավասար է -ի:

Կարելի է պատկերացնել նաև այնպիսի անկյուն, որի մեծությունը է:

Լրիվ անկյան քառորդ մասը կամ փռված անկյան կեսը կոչվում է ուղիղ անկյուն, որի մեծությունը հավասար է -ի:
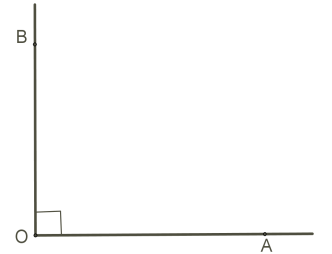
Այն անկյունը, որի մեծությունը՝ կոչվում է սուր անկյուն:
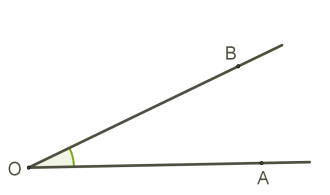
Այն անկյունը, որի մեծությունը՝ կոչվում է բութ անկյուն:

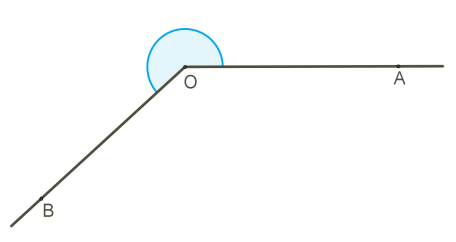
Այն անկյունը, որի մեծությունը՝ կոչվում է բացված անկյուն:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի.Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: