1. Ճառագայթ և անկյուն

 

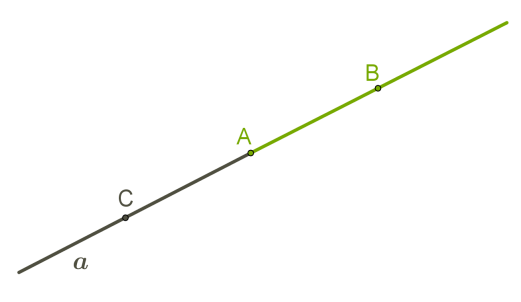
\(A\) կետը \(a\) ուղիղը բաժանում է երկու ճառագայթի: Կարևոր է տարբերել այդ ճառագայթներն իրարից: Այդ նպատակով ուղղի վրա վերցնենք ևս երկու կետ՝ \(B\)-ն և \(C\)-ն, և ճառագայթները նշանակենք համապատասխանաբար \(AB\) և \(AC\):

 

Վերևի նկարում երեք կետերից յուրաքանչյուրը կարող է դիտարկվել որպես ճառագայթի սկզբնակետ: Յուրաքանչյուր կետից՝ հակառակ ուղղություններով, դուրս են գալիս երկու ճառագայթներ և անվերջ շարունակվում: 

 

 

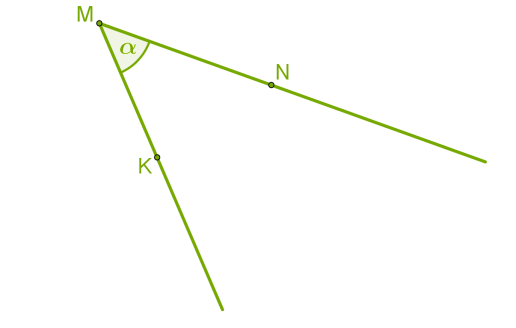
Անկյունները, հիմնականում նշանակում են լատիներեն մեծատառերով, օրինակ՝$\measuredangle \mathit{KMN}$ կամ հունարեն փոքրատառերով, օրինակ՝ $\mathrm{\alpha }$:

 

 

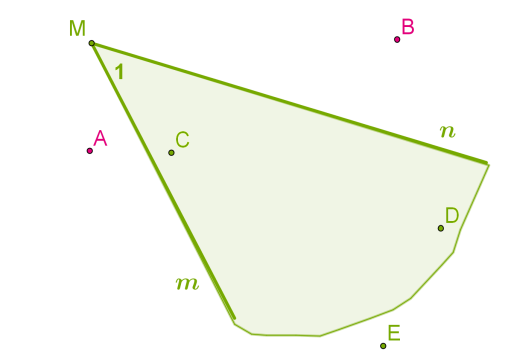
Վերևի նկարի՝ \(M\) ընդհանուր սկզբնակետով \(n\) և \(m\) ճառագայթները հարթությունը բաժանում են երկու մասի, որոնք կոչվում են անկյան ներքին և արտաքին տիրույթներ:

Հետևաբար, վերևի նկարի \(A\) և \(B\) կետերը չեն պատկանում$\measuredangle M$ անկյանը, իսկ \(C\), \(D\) և \(E\) կետերը պատկանում են $\measuredangle M$ անկյանը:

 

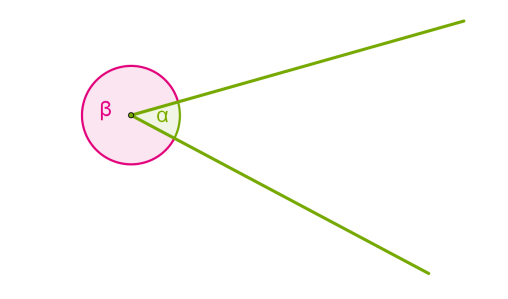
Եթե գծենք նույն սկզբնակետից դուրս եկող երկու ճառագայթներ, ապա ներքին տիրույթը կկազմի մի անկյուն (ներքևի նկարի $\mathrm{\alpha }$ անկյունը), իսկ արտաքինը՝ մեկ ուրիշ ($\mathrm{\beta }$-ն):

 

 

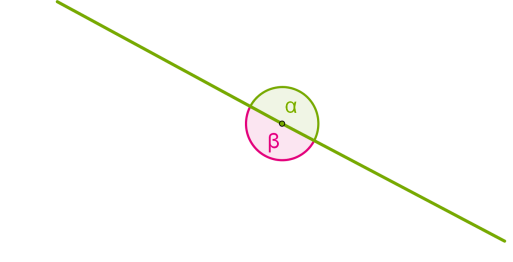
Եթե $\measuredangle A$ անկյան գագաթից ներքին տիրույթում տանենք ճառագայթ, ապա այն կբաժանի անկյունը երկու այլ անկյունների:

 

 

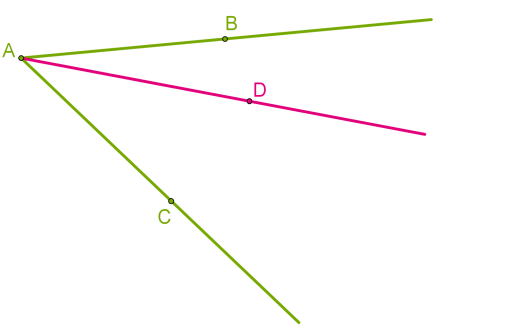
Այս դեպքում կարևոր է հետևել անկյունների նշանակումներին: Հիմա մենք ունենք սկզբնական անկյունը և նրա երկու մասերը: Օրինակ՝ եթե գրենք այսպես՝$\measuredangle A$, ապա չի հասկացվի, թե որ անկյունը մենք նկատի ունենք: Այս դեպքում հարմար է օգտագործել անկյունների նշանակումները երեք լատիներեն մեծատառերի միջոցով՝$\measuredangle \mathit{CAB}$, $\measuredangle \mathit{CAD}$, $\measuredangle \mathit{DAB}$: