2. Եռանկյունների հավասարության երկրորդ հայտանիշի կիրառումը

54 սմ հիմքով հավասարասրուն եռանկյան մեջ տարված է$\measuredangle \mathit{ABC}$ անկյան կիսորդը: Օգտագործելով եռանկյունների հավասարության երկրորդ հայտանիշը` ապացուցիր, որ \(BD\) հատվածը հանդիսանում է միջնագիծ և որոշիր \(AD\) հատվածի երկարությունը:

 

 

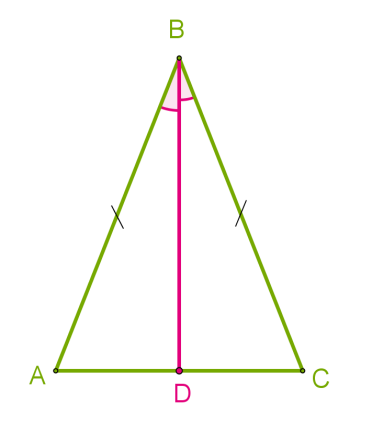
Դիտարկենք $\mathrm{\Delta }$$\mathit{ABD}$ և $\mathrm{\Delta }$ եռանկյունները:

 

1. Քանի որ հավասարասրուն եռանկյան հիմքին առընթեր անկյունները հավասար են, ապա$\measuredangle$$A$\(=\)$\measuredangle$

 

2. Քանի որ տարված է կիսորդ, ապա $\measuredangle$\(=\)$\measuredangle$$\mathit{CBD}$

 

3. Քանի որ տրված $\mathrm{\Delta }$\(ABC\) եռանկյունը  է, ապա $\mathrm{\Delta }$$\mathit{ABD}$ և $\mathrm{\Delta }$$\mathit{CBD}$ եռանկյուններն ունեն մեկական հավասար կողմ՝ \(AB = CB\):

 

Ըստ եռանկյունների հավասարության երկրորդ հայտանիշի $\mathrm{\Delta }$$\mathit{ABD}$ և $\mathrm{\Delta }$$\mathit{CBD}$ եռանկյունները հավասար են:

 

Հետևաբար, հավասար են բոլոր համապատասխան մեծությունները, մասնավորապես՝ \(AD = CD\): Սա նշանակում է, որ \(BD\) հատվածը տրված եռանկյան միջնագիծն է և կիսում է \(AC\) կողմը:

 

\(AD =\)  սմ: