13. Եռանկյունների երկու զույգերի հավասարության ապացուցումը

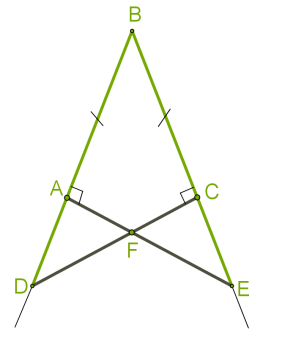
$\measuredangle$\(ABC\) անկյան կողմերի վրա վերցված են \(A\) և \(C\) կետերը, որոնք գտնվում են հավասար հեռավորությունների վրա գագաթից՝ \(BA = BC\): Այդ կետերով անկյան կողմերին տարված են ուղղահայացներ՝ \(AE\)$\perp$\(BA\), \(CD\)$\perp$\(BC\):

 

1. Ապացուցիր եռանկյունների հավասարությունը՝ $\mathrm{\Delta }$\(AFD\) և $\mathrm{\Delta }$\(CFE\):

 

2. Որոշիր այն անկյան մեծությունը, որի տակ \(CD\) ուղղահայացը հատում է \(BA\)-ն, եթե \(AE\)-ն հատում է \(BC\)-ն 64$\mathrm{°}$ անկյան տակ:

 

1. Ո՞ր եռանկյունների հավասարության միջոցով կապացուցվի $\mathrm{\Delta }$\(AFD\) և $\mathrm{\Delta }$\(CFE\) եռանկյունների հավասարությունը՝

 

$\mathrm{\Delta }$\(B\)\(A\)\(=\)$\mathrm{\Delta }$

 

Ո՞ր հայտանիշի միջոցով է ապացուցվում այդ հավասարությունը:

Նշիր այն տարրերը, որոնց հավասարությունը թույլ է տալիս $\mathrm{\Delta }$\(AFD\) և $\mathrm{\Delta }$\(CFE\) եռանկյուններում կիրառել ընտրված հայտանիշը: 

 

Անկյուններ՝                 Կողմեր՝

• \(CEF\)
• \(FAD\)
• \(FCE\)
• \(ADF\)
• \(DFA\)
• \(EFC\)

                

• \(FA\)
• \(DF\)
• \(AD\)
• \(EF\)
• \(CE\)
• \(FC\)

 

2. Անկյան մեծությունը, որի տակ \(CD\) ուղղահայացը հատում է \(BA\)-ն $\mathrm{°}$ է: