1. Եռանկյունների հավասարության երկրորդ և երրորդ հայտանիշները

 

 

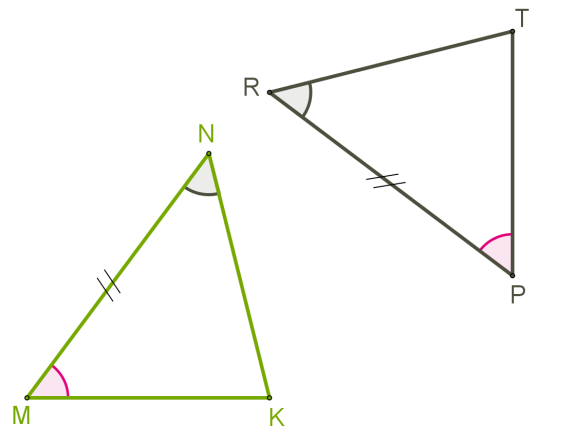
Ինչպես և առաջին հայտանիշը ապացուցելիս, այստեղ ևս պետք է համոզվել, որ ենթադրությունները բավարար են, որպեսզի եռանկյունները հավասար լինեն՝ համընկնեն վերադրումով:

1. Քանի որ $\mathit{MN}=\mathit{PR}$, ապա այդ հատվածները կհամընկնեն, եթե վերադրենք դրանց ծայրակետերը:

 

2. Քանի որ$\measuredangle N=\measuredangle R$ և $\measuredangle M=\measuredangle P$, ապա \(MK\) և \(NK\) ճառագայթները կհամընկնեն համապատասխանաբար \(PT\) և \(RT\) ճառագայթների հետ:

 

3. Եթե համընկնում են ճառագայթները, ապա համընկնում են նաև դրանց հատման \(K\) և \(T\) կետերը:

 

4. Այսպիսով, համընկան եռանկյունների բոլոր գագաթները, այսինքն՝ համընկան $\mathrm{\Delta }\mathit{MNK}$ և $\mathrm{\Delta }\mathit{PRT}$ եռանկյունները, հետևաբար, դրանք հավասար են:

 

 

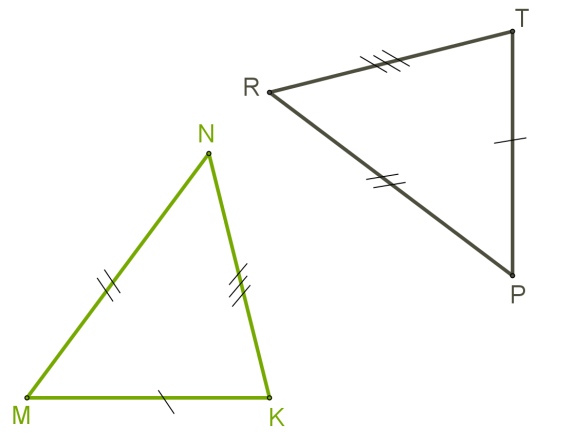
Նորից փորձենք վերադրել $\mathrm{\Delta }\mathit{MNK}$ և $\mathrm{\Delta }\mathit{PRT}$ եռանկյունները այնպես, որ դրանք համընկնեն: Համոզվենք, որ կողմերի հավասարությունն ապահովում է այդ եռանկյունների համապատասխան անկյունների հավասարությունը, ինչից էլ կհետևի, որ եռանկյունները համընկնում են:

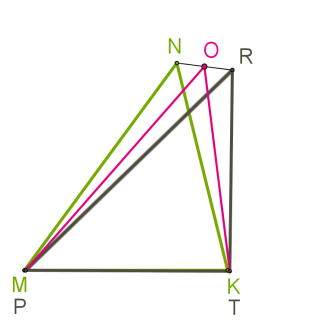
Վերադրենք, օրինակ, \(MK\) և \(PT\) հավասար կողմերն այնպես, որ դրանք համընկնեն: Կատարենք հակասող ենթադրություն, որ \(N\) և \(R\) կետերն այդ ընթացքում չեն համընկնում:

Դիցուք \(O\)-ն \(NR\) հատվածի միջնակետն է: Տրված է, որ $\mathit{MN}=\mathit{PR}$ և $\mathit{KN}=\mathit{TR}$: \(MNR\) և \(KNR\) եռանկյունները հավասարասրուն են՝ \(NR\) ընդհանուր կողմով: Հետևաբար դրանց \(MO\) և \(KO\) միջնագծերը հանդիսանում են նաև բարձրություններ և ուղղահայաց են \(NR\)-ին: \(MO\) և \(KO\) ուղիղները չեն համընկնում, քանի որ \(M\), \(K\), \(O\) կետերը նույն ուղղի վրա չեն: Բայց \(NR\) ուղղի \(O\) կետով անցնում է միայն մեկ ուղիղ, որը ուղղահայաց է \(NR\) ուղղին: Եկանք հակասության: Ապացուցեցինք, որ \(N\) և \(R\) գագաթները ևս համընկնում են: