
















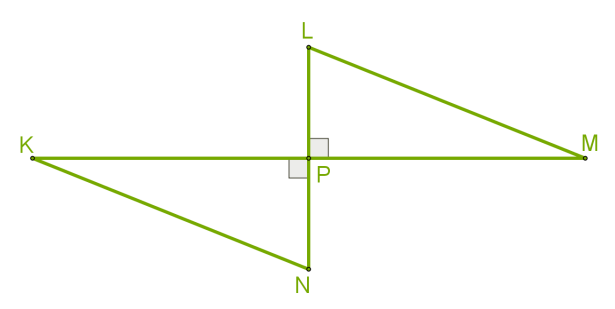
\(KM\) և \(LN\) ուղղահայաց հատվածները հատվում են \(P\) ընդհանուր կետում:
Որքա՞ն են\(N\) և \(K\) անկյունների մեծությունները, եթե \(L\) \(=\) 35 և \(M\) \(=\) 55:
Նկատի ունեցիր, որ գծագիրը ճշգրիտ չէ:
1. Հատվածները կիսվում են, հետևաբար՝ \(KP\)\(=\) ,\(=\) \(LP\), \(=\) \(MPL\), քանի որ ուղիղները ուղղահայաց են, և երկու անկյունն էլ հավասար են -ի:
Ըստ եռանկյունների հավասարության առաջին հայտանիշի՝ \(KPN\) և \(MPL\) եռանկյունները հավասար են:
2. Հավասար եռանկյուններում համապատասխան անկյունները հավասար են:
Այս եռանկյուններում համապատասխան են՝ և \(M\), և \(L\)՝
\(K\) \(=\)
\(N\) \(=\)